Universidad de Colima, Colima, México
*jesus_larios@ucol.mx
![]() Jesús Antonio Larios Trejo*
Jesús Antonio Larios Trejo*
Universidad de Colima, Colima, México
*jesus_larios@ucol.mx
Recibido el 10 de abril de 2025, aceptado el 10 de abril de 2025.
Este artículo fue invitado por el comité editorial y, en consecuencia, está exento de revisión por pares a doble ciego. Su contenido es responsailidad exclusiva de los autores.
El modelado matemático proporciona a los futuros maestros una comprensión práctica de los conceptos matemáticos, permitiéndoles aplicarlos mediante actividades que apelen a otras áreas del conocimiento, a fin de enseñar matemáticas de manera efectiva. La enseñanza de esta disciplina debe ir más allá de la memorización de fórmulas, e involucrar a los estudiantes en la resolución de problemas reales a través de modelos matemáticos. Este trabajo presenta la aplicación de un experimento que involucra la química con el fin de desarrollar habilidades de modelado por medio de una metodología centrada en la experimentación y el descubrimiento. Se detallan la propuesta, las actividades y los elementos considerados para su implementación con los profesores en formación de la Licenciatura en Enseñanza de las Matemáticas de la Universidad de Colima, México. Es necesario resaltar que el modelado matemático favorece el desarrollo del pensamiento crítico y las habilidades analíticas en los docentes en formación, preparándolos para enfrentar los diversos desafíos que pueden surgir en el aula. Se concluye que la integración del modelado matemático en los programas de formación docente es elemental, pues contribuye a elevar la calidad de la enseñanza de las matemáticas en niveles educativos básicos y superiores. Su impacto es aún más beneficioso cuando se establece una conexión con otras disciplinas.
Palabras clave: didáctica, enseñanza de las matemáticas, experimento, modelado matemático, profesor de matemáticas, transversalidad de las ciencias.
Mathematical modeling provides future teachers with a practical understanding of mathematical concepts, allowing them to apply these concepts through activities that connect with other areas of knowledge in order to teach mathematics effectively. The teaching of this discipline should go beyond the memorization of formulas and involve students in solving real-world problems through mathematical models. This paper presents the application of an experiment that incorporates chemistry with the aim of developing modeling skills through a methodology centered on experimentation and discovery. The proposal, activities, and elements considered for its implementation with preservice teachers in the Bachelor’s Degree in Mathematics Education at the University of Colima, Mexico, are detailed. It is important to highlight that mathematical modeling fosters the development of critical thinking and analytical skills in preservice teachers, preparing them to face the various challenges that may arise in the classroom. The study concludes that integrating mathematical modeling into teacher education programs is essential, as it contributes to improving the quality of mathematics education at both basic and higher levels. Its impact is even more beneficial when connections are established with other disciplines.
Keywords: didactics, mathematics teaching, experiment, mathematical modeling, mathematics teacher, transversality of sciences.
El plan de estudios de la Licenciatura en Enseñanza de las Matemáticas (LEM) de la Universidad de Colima busca ofrecer una formación integral con perspectiva humanista, que abarque tanto el campo disciplinar como las competencias específicas. En consecuencia, se enfoca en generar ciudadanos comprometidos con su desarrollo personal, así como con su entorno social, al tiempo que responde las necesidades primarias del sistema educativo. A partir de lo anterior, la LEM tiene por objetivo:
formar profesionales con competencias que les permitan identificar y resolver problemas relacionados con la enseñanza y el aprendizaje de las matemáticas para ejercer la docencia, desarrollar proyectos, generar ambientes de aprendizaje, utilizar elementos técnico-metodológicos y medios didácticos innovadores, que promuevan la alfabetización matemática, con alto sentido de responsabilidad social. (Universidad de Colima, 2015, p. 49)
Entre enero y julio de 2024, en el sexto semestre, se ofertó la asignatura optativa de Modelado matemático, con el objetivo de:
[contribuir] al desarrollo de competencias que permiten identificar y resolver problemas relacionados con la enseñanza y el aprendizaje de las matemáticas para ejercer la docencia con base en el análisis y resolución de situaciones de diversos contextos utilizando diversos pensamientos matemáticos. (Universidad de Colima, 2015, p. 181)
La formación de docentes en matemáticas debe contemplar el desarrollo de habilidades de modelado matemático, puesto que resultan fundamentales para su práctica profesional. Contar con estos elementos en el programa formativo les permitirá a los profesores, a la postre,encaminar a sus estudiantes en la resolución de problemas del mundo real (Pollak, 2007). De este modo, se busca promover situaciones que sean familiares para el alumnado de los distintos niveles educativos.
Tales habilidades se fortalecen al introducir al futuro profesor de matemáticas ensituaciones de modelado. Como lo apuntalan Kaiser y Schwarz (2006), “los futuros docentes deben experimentar el proceso de modelización matemática para poder comprender y enseñar cómo las matemáticas pueden aplicarse a problemas del mundo real” (p. 89). Por tal razón, además de las asignaturas de corte disciplinar, resulta imperativo integrar materias de enfoque pedagógico en las que se vinculen las estrategias de enseñanza con la disciplina matemática.
El modelado matemático tiene un propósito patente en los distintos niveles educativos durante la formación básica o media superior, pero también ostenta prominencia en áreas como las ingenierías y las licenciaturas. Su valor radica en quepermite captar la atención de los pupilos hacia nuevos conceptos y procedimientos matemáticos, acercándolos a contextos más contundentes para ellos. Por dicha razón, se promueve emplear escenarios reales que aprovechen el potencial del modelado matemático para que el alumno comprenda y resuelva problemas de su entorno, favoreciendo el aprendizaje sobre la pertinencia de las matemáticas (Kaiser y Stender, 2013).
Según Pollak (1977), la modelación hace posible visualizar los problemas y motiva a la comunidad educativa a solucionar situaciones cercanas a su entorno. Por su parte, Greefrath y Vorhölter (2016) describen la modelación como un proceso cíclico que abarca tres momentos: el mundo real, el mundo matemático y el regreso al mundo real. Además, Blum (2015) enfatiza que “la modelización matemática no es solo una herramienta para resolver problemas, sino un medio para establecer una comprensión profunda de los conceptos matemáticos y su aplicación en contextos diversos” (p. 187).
Para el abordaje del modelado Blum y Leiß (2007) proponen el siguiente procedimiento cíclico:
a) Comprender la instrucción y la situación real (modelo de situación).
b) Formular suposiciones y simplificar el modelo de la situación (construcción de un modelo real).
c) Matematizar el modelo real, es decir, elaborar un modelo matemático en función de la información obtenida.
d) Trabajar dentro del modelo matemático (resolución de los procesos matemáticos).
e) Interpretar la solución (el problema no se resuelve únicamente con un número, sino mediante una reflexión sobre la situación).
f) Validar la solución interpretada (corroborar los resultados y la conclusión)
g) Exponer el resultado, presentando el proceso y los hallazgos.
Es menester enfatizar que se trata de un mecanismo cíclico: la situación o la reflexión pueden acarrear un nuevo proceso de modelación. Tras revisar a diversos autores que abordan el proceso del modelado matemático, se identifican varios puntos de coincidencia:
Comprensión del problema: Blum y Niss (1991) mencionan que, en un primer momento, se debe comprender la situación problemática y definir claramente los objetivos a alcanzar. En esta primera fase se identifican y enmarcan las tareas dentro de un contexto del mundo real, se recopilan datos relevantes, se clarifican las necesidades y se determina el propósito del modelado.
Construcción del modelo: según Lesh y Doerr (2003), en esta etapa, a partir de la información recabada, se construye un modelo mediante la representación matemática de la situación real. A tal efecto, los sujetos deben disponer de la información, plantear ecuaciones, identificar variables y establecer las relaciones matemáticas que puedan proporcionar sentido a la problemática.
Resolución del problema: es el momento donde se aplican los conocimientos matemáticos disponibles, lo cual implica el conocimiento del algebra, cálculo, estadística u otros recursos pertinentes que habiliten comprender el fenómeno o la situación planteada. Pollak (2007) sostiene que la resolución del modelo es una secuencia ciclica de prueba y refinamiento orientada a alcanzar resultados satisfactorios.
Interpretación de los resultados: Kaiser y Stender (2013) explican que interpretar los resultados es fundamental para que el modelo sea funcional. No se trata únicamente de obtener soluciones o realizar proyecciones, sino de contextualizar su significado en el marco de la situación planteada.
Validación del modelo: Blum y Leiß (2007) subrayan que la validación es primordial, ya que asegura que el modelo sea aplicable para la situación planteada, pero que además sea capaz de adaptarse a diferentes variables y predecir comportamientos. Es en este momento cuando se comparan las predicciones del modelo contra la realidad con el fin de evaluar su precisión y fiabilidad.
Refinamiento y reiteración: Los modelos requieren, frecuentemente, ajustes y mejoras. Este paso consiste en revisar los procesos previos, realizar modificaciones necesarias y plantearse preguntas orientadas a esclarecer desde el modelo hasta su aplicación.
Comunicación del modelo: Blum y Ferri (2009) destacan la importancia de transmitir los resultados de forma clara y comprensible a públicos académicos y no especializados. La finalidad es que los hallazgos puedan entenderse con precisión y contribuyan a la comprensión de situaciones de todo tipo.
Tales pasos ofrecen una estructura general para abordar problemas de modelado matemático, al mismo tiempo que facilitan una revisión sostenida del modelo y de la situación planteada. La enseñanza en la modelización matemática se basa en tres pilares clave: algebraico, numérico y gráfico, mediante los cuales se pueden visualizar los diferentes aspectos del problema. Dichos enfoques impulsan a los los alumnos a experimentar con diferentes representaciones de una misma situación, lo que enriquece su comprensión y su capacidad de resolución. Además, al favorecer la internalización profunda de los conocimientos matemáticos, incentivan a los estudiantes a contemplar los problemas a partir de múltiples puntos de vista, aspecto esencial para su desarrollo cognitivo y su capacidad para aplicar elconocimiento en contextos del mundo real. Conforme a ello, Blum (2015) enfatiza que la modelización matemática debe concebirse como una actividad cognitiva crucial, orientada a la creación de herramientas que permitan al alumnado entender y manejar de manera eficaz las situaciones reales, presentes o futuras.
Según Blum, el propósito de esta actividad es fomentar una competencia matemática relevante, valiosa para la cultura y la sociedad, al tiempo que compatible con los fines educativos. Tal visión cognitiva de la modelización refuerza la importancia de integrar estas actividades en la formación docente, ya que prepara a los futuros maestros para guiar a sus alumnos en la asimilación y aplicación de las matemáticas de manera que impacte en su vida cotidiana y en su relación con el mundo.
En la revisión literaria se advierte que, al abordar el modelado, se apuntala consistentemente la participación activa tanto de la comunidad estudiantil como del profesorado, lo cual se relaciona con un aprendizaje sustentado en la construcción del conocimiento. Empero, el modelado puede articularse dentro de un enfoque de aprendizaje basado en proyectos, una de las líneas promovidas actualmente por la Secretaría de Educación Pública en México. En tal sentido, Guerrero y Terrones (2003) establecen que:
Los proyectos permiten a los alumnos desarrollar competencias, así como habilidades específicas para planificar, organizar y llevar a cabo una tarea común en entornos reales. Así, se organizan en equipos de trabajo, asumen responsabilidades individuales y grupales, realizan indagaciones o investigaciones, solucionan problemas, construyen acuerdos, toman decisiones y colaboran. (p. 53)
Por otro lado, Maass y Engeln (2018) refieren que los diseños de proyectos enfocados a los experimentos de enseñanza se resumen en tres puntos:
La enseñanza se orienta a que el tema de investigación tenga relevancia para los estudiantes y su vida cotidiana; por ello, los entornos de aprendizaje deben ser auténticos y conectados con la realidad.
Se fomenta que los alumnos observen fenómenos, formulen sus propias preguntas, seleccionen herramientas pertinentes, realicen experimentos, busquen explicaciones, interpreten y evalúen soluciones; en este proceso, los estudiantes asumen un rol activo en su propio aprendizaje.
La dinámica del aula se transforma; en lugar de estar centrada en el docente se centra en el estudiante, promoviendo su participación activa y autonomía en el proceso educativo.
Según Santana Ortega et al. (2018), la experimentación en matemáticas implica realizar actividades físicas que permitan a los pupilos interactuar directamente con sistemas experimentales, ya sea en contextos químicos o físicos. Dicha interacción favorece la construcción del conocimiento matemático y el fortalecimiento de las habilidades del pensamiento científico. Por otra parte, complementan esta visión al destacar que el aprendizaje debe analizarse en contextos específicos y utilizando estrategias y herramientas que integren los procesos de aprendizaje, enseñanza y evaluación de forma articulada.
La investigación de diseño en la enseñanza y el modelado matemático presenta características fundamentales orientadas a optimizar el aprendizaje del alumnado. Conforme a Blum (2015), el centro debe ser el estudiante, y la gestión del aula debe potenciar el tiempo, los recursos y fomentar el trabajo colaborativo. Dicha perspectiva promueve un entorno social e intelectualmente estimulante, dentro del cual los errores se resiginifican como oportunidades de aprendizaje. Así, se refuerza la idea de que una respuesta incorrecta puede ser la puerta correcta a nuevas preguntas.
Además, es menester que los estudiantes se mantengan cognitivamente activos. Dicho aspecto implica trascender la observación e involucrarse de manera consciente y reflexiva en el proceso de modelado, asegurando un equilibrio entre la autonomía del alumno y la guía del profesor. La metacognición ocupa un papel angular en esta causa, ya que abre el análisis de las propias estrategias de aprendizaje y ajustarlas para desarrollar una comprensión más profunda. El empleo de ejemplos variados, asimismo, tanto en el ámbito matemático como en contextos reales, resulta esencial para evitar la dependencia de un solo escenario y favorecer la transferencia del conocimiento a múltiples situaciones.
Otro aspecto destacado es la necesidad de fomentar soluciones individuales a las tareas, lo cual diversifica los enfoques y permite comparaciones desde un nivel metacognitivo. Tal perspectiva favorece la diferenciación interna en el aula y refleja la naturaleza dinámica y plural de las matemáticas. Cabe añadir que las competencias en modelado se desarrollan progresivamente, comenzando desde la educación primaria y extendiéndose de manera continua mediante una práctica repetitiva e integrada que busca un equilibrio entre las subcompetencias y la competencia global en modelado.
La evaluación debe alinearse con los objetivos del modelado y sus aplicaciones, empleando métodos variados para llevar a cabo un diagnóstico de las fortalezas y las áreas de oportunidad del estudiantado. Por consecuencia, el presente enfoque implica también la adquisición paralela de competencias, creencias y actitudes hacia las matemáticas. Por ende, las tecnologías digitales y computadoras se consolidan como herramientas dentro de la actividad de modelado, ampliando el ciclo tradicional al incorporar un tercer ámbito: el mundo tecnológico.
Diversos estudios de caso han demostrado que una enseñanza de calidad puede expandir las creencias del alumnado sobre las matemáticas y fortalecer su capacidad para comprender y aplicar modelos correspondientes. Investigar el diseño de la enseñanza del modelado constituye un acercamiento integral que exige la activación cognitiva y metacognitiva. Asimismo, la incorporación de contextos variados y auténticos, la promoción de soluciones individuales y la integración de tecnologías digitales resultan imperativas para el asentamiento de competencias a largo plazo.
La presente investigación de corte exploratorio permite describir y analizar cómo se adquieren los conocimientos matemáticos mediante la observación y la aplicación de una secuencia didáctica. A través de una aproximación cualitativa, se buscó describir los resultados tras la ejecución con alumnos de la Licenciatura en Enseñanza de las Matemáticas, de la Facultad de Ciencias de la Educación. Participaron activamente 18 alumnos del sexto semestre, quienes desempeñaron las actividades propuestas durante tres semanas de clases. En dicho periodo, se llevó a cabalidad una secuencia de fases que facilitaron observar el proceso de modelado matemático correspondiente a la cristalización de sales minerales. El análisis de los datos consistió en la descripción de cada una de las fases implementadas en la secuencia didáctica.
Se diseñó una secuencia didáctica orientada al desarrollo de un modelo que integra conocimientos de ciencias naturales y matemáticas. Para ello, se optó por la ejecución de experimentos con la ayuda del kit Magic Rocks, comercializado por el Instituto Smithsonian. Este material permite cultivar cristales, lo que resulta atractivo para niños y niñas al posibilitar la creación de un jardín de cristales brillantes. La secuencia se esquematiza en la Figura 1.
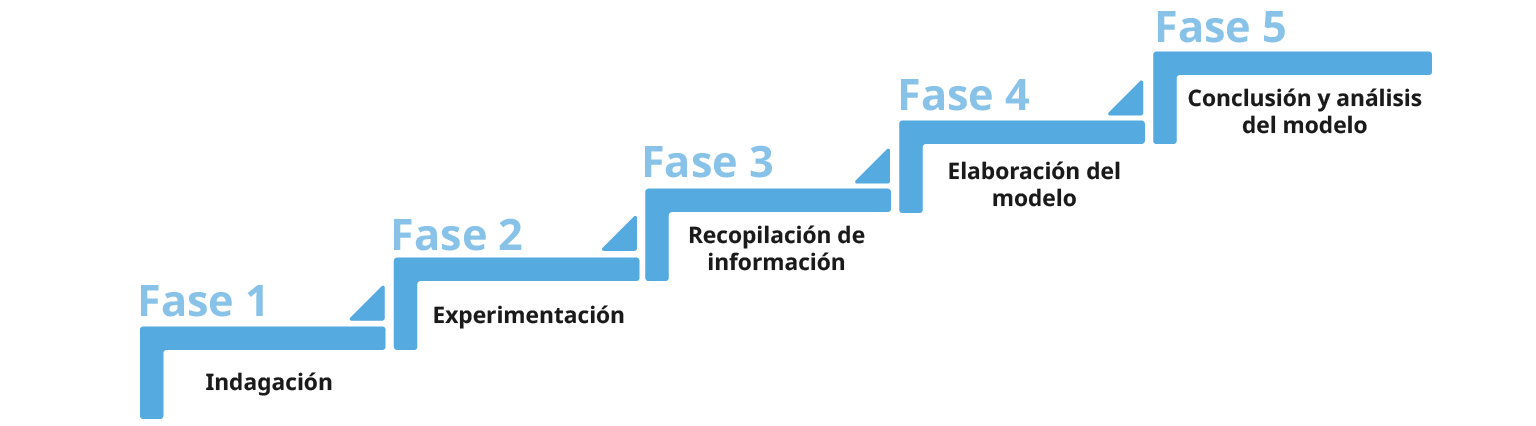
Figura 1. Proceso del modelado con énfasis en química.
El experimento base propuesto se denomina “Cultivo de rocas mágicas” y tiene como propósito que infantes y adultos observen en tiempo real la formación de cristales (Figura 2). Esta actividad representa un ejemplo del proceso de cristalización, un fenómeno natural en el que las partículas disueltas en una solución o en un material fundido se organizan de manera estructurada y repetitiva, dando lugar a la configuración de cristales tras un tiempo dado. Tal lapso será aprovechado por los alumnos para observar y medir el crecimiento de los cristales, considerando variables como la temperatura y las cantidades de solución empleada. El kit Magic Rocks es apto para comunidades estudiantiles de diversas edades y contiene los elementos indispensables para ejecutar el procedimiento de forma segura y controlada, entre ellos:
1) Sales metálicas: pequeños fragmentos que se colocan en el fondo del recipiente y actúan como puntos de nucleación, semillas desde las cuales emergen y crecen los cristales.
2) Imagen de fondo: ilustración decorativa que permite observar la formación de los cristales y ofrece un contraste visual que resalta el fenómeno.
3) Solución mágica: mezcla saturada de compuestos químicos que, bajo las condiciones adecuadas, inicia el proceso de cristalización.
4) Silicato de sodio: componente clave que regula la velocidad y la forma del crecimiento cristalino; da pie a una formación estructurada y observable.
5) Hoja de etiquetas: conjunto de elementos adicionales con los cuales identificar, clasificar y organizar los materiales y las sustancias utilizadas.
6) Tanque para cultivo: recipiente transparente destinado a contener el proceso de cristalización. Debe estar limpio y seco para evitar contaminaciones, y ser resistente a altas temperaturas, ya que se requiere agua caliente para activar la reacción.
7) Instructivo: aunque el docente proporciona las indicaciones para la elaboración del experimento, el kit también incluye un manual detallado. El instructivo garantiza que cualquier participante que desee realizar la actividad de forma autónoma pueda hacerlo sin riesgo de sufrir daño.

Figura2. Reverso del kit Magic Rocks del Smithsonian.
Los futuros docentes de matemáticas llevaron a cabo un proceso de investigación previa en el cual se les solicitó indagar y reflexionar acerca de los fenómenos que estaban por observar. Esta fase resultó de suma importancia para comprender la base científica que sustenta la cristalización, es decir, el vínculo entre conceptos químicos y matemáticos. En principio, la etapa se orientó en dos sentidos: la comprensión de la naturaleza del experimento y del proceso químico que se realizó, y la aplicación en contexto del fenómeno de cristalización.
Primero, los alumnos tenían que averiguar en qué consiste y cómo se manifiesta la cristalización en la naturaleza. En dichas búsquedas recurrieron a fuentes como libros de química y biología, así como a videos del propio experimento. El acceso a las fuentes fue libre, por lo que los participantes podían aprovechar motores de búsqueda y todo recurso a su alcance. También se les asignó identificar ejemplos de cómo se llevan a cabo dichos procesos de cristalización. Después, se profundizó en conceptos como solubilidad, saturación, nucleación y crecimiento cristalino, que más adelante servirían como variables para comprender el fenómeno. Además, se analizaron las condiciones necesarias para la formación de cristales, incluyen-do los factores que controlan su tamaño y estructura.
La comunidad estudiantil investigó ejemplos donde este proceso ocurre de manera natural o industrial. Se relacionó el experimento con contextos reales, como la formación de cristales de sal en cuerpos de agua evaporados, la cristalización del azúcar en la elaboración de caramelos o su aplicación industrial en la extracción minera. El objetivo fue conocer el fenómeno, registrarlo y compararlo con loexperimentado. Al final, estas observaciones serían socializadas con el grupo.
A partir de este proceso de indagación fue posible estructurar el experimento y reflexionar sobre cómo diseñar una estrategia didáctica basada en la investigación y la experiencia directa. Así, los futuros docentes integraron una visión interdisciplinar donde ciencias como las matemáticas, la química y la pedagogía se enlazan, brindando herramientas para enseñar fenómenos científicos a través de experiencias prácticas y visuales.
Con la información recopilada, los futuros docentes de matemáticas debieron generar las condiciones necesarias para la ejecución del experimento. Además de seguir las indicaciones del instructivo, analizaron todas las variables involucradas en el proceso. Para ello, los equipos realizaron las siguientes acciones:
Los alumnos identificaron el espacio más adecuado para realizar el experimento, asegurándose de que contara con iluminación tenue, ventilación (debido al uso de químicos volátiles) y una superficie firme donde apoyar el recipiente. Se optó por una mesa estable que evitara movimientos bruscos, ya que se precisa inmovilidad durante la cristalización. Para proteger la superficie de trabajo, se dispuso una hoja de papel aluminio —aunque también puede utilizarse un mantel plástico como alternativa práctica— para evitar daños por derrames de la solución.
Los alumnos colocaron agua en un recipiente de cristal y la calentaron hasta quealcanzó la temperatura idónea para disolver la solución incluida en el kit (para garantizar precisión, fue imprescindible el empleo de un termómetro). El contenedo de cristal fue elegido tanto por su capacidad térmica como por su transparencia, la cual facilita la observación del proceso. Cabe notar que puede dividirse la solución en varios recipientes pequeños para comparar el crecimiento de los cristales bajo diferentes condiciones térmicas.
Una vez que el agua estuvo caliente, se vertió la solución proporcionada en el kit dentro del recipiente de cristal. Antes de agregar las piedras, fue necesario mezclar de manera constante para asegurar que la disolución fuera transparente y homogénea; al final, estas actuaron como núcleos, permitiendo que los cristales comenzaran a formarse y crecer sobre su superficie.
Tras colocar la solución y las piedras en el interior del recipiente, los alumnos debieron monitorear y registrar los cambios que se producían dentro del contenedor en distintos momentos. El recipiente fue dispuesto donde pudiera observarse sin sufrir movimientos bruscos ni interrupciones. Se procuró que el espacio estuviera protegido de la luz solar directa para evitar interferencias en el proceso
A medida que la solución perdía temperatura y el agua se evaporaba, los compuestos en la solución comenzaron a cristalizarse sobre las piedras. Durante las primeras horas, los participantes atestiguaron la formación inicial de los cristales, documentaron el proceso con fotografías y registraron sus observaciones en intervalos regulares. Se lograron reconocimientos de patrones de crecimiento (la altura de los cristales en relación con el tiempo transcurrido), lo que facilitó contrastar los datos con las predicciones realizadas en la fase de investigación.
Transcurridas varias horas de monitoreo, los cristales alcanzaron su crecimiento máximo, determinado por el nivel del agua en el recipiente. Las piedras yacieron en la solución hasta que los cristales se solidificaron por completo. Al concluir, los alumnos analizaron las propiedades físicas de los cristales formados, como textura y estructura.
En este caso, el experimento empleó cristales de sal metálica en una solución de silicato de sodio, un material comúnmente conocido como “agua de cristal” o “vidrio líquido”. La cristalización ocurre de la siguiente manera
1) La solución de silicato de sodio alcanza un estado de saturación; en ese momento, las partículas disueltas comienzan a unirse en una estructura ordenada.
2) Los excesos de soluto se depositan sobre las piedras metálicas, posibilitando el crecimiento de los cristales.
3) El tiempo de exposición y las condiciones ambientales influyen directamente en la forma y el tamaño de los cristales obtenidos.
Comprender este proceso permitió a los equipos comparar los resultados entre sí, analizando qué factores pudieron haber influido en el crecimiento de los cristales, como la temperatura del agua, el tipo de recipiente o la preparación del área de trabajo. Entre las variables clave identificadas se destacan
1) Temperatura de la solución: una mayor temperatura favorece una cristalización más abundante.
2) Tiempo de reposo: con el tiempo, los cristales tuvieron oportunidad decrecer con mayor solidez y uniformidad.
3) Distribución de las piedras: aunque los kits incluían cantidades similares de material, se observó que los equipos que distribuyeron las piedras con mayor espacio entre sí, o que emplearon fragmentos más grandes, obtuvieron cristales con mayor dureza y mejor formación (Figura 3).

Figura 3. Evidencia del experimento.
Los equipos asumieron la responsabilidad de recolectar la información necesaria para revisar el comportamiento del proceso de cristalización. Uno de los factores fue la temperatura del agua, la cual disminuía progresivamente hasta alcanzar la del ambiente, afectando de manera visible el crecimiento de los cristales en los recipientes. Con el fin de sondear estos cambios, los equipos establecieron intervalos regulares de tiempo y utilizaron instrumentos de medición, como termómetros digitales. Asimismo, registraron el desarrollo de los cristales en términos de altura, grosor y patrones de crecimiento en distintas zonas del recipiente.
Cada equipo determinó sus propias estrategias para la recopilación de datos, seleccionando las variables que consideraron más relevantes. Algunos se enfocaron en medir la altura del crecimiento cristalino, mientras que otros optaron por registrar la temperatura a intervalos de 3 o 5 minutos. También hubo equipos que eligieron identificar cambios más prolongados, realizando mediciones cada 10 o 12 minutos. Además, los equipos consideraron otros factores de análisis como:
1) La velocidad de cristalización en diferentes zonas del tanque.
2) La intensidad y uniformidad del color de los cristales.
3) La regularidad morfológica de los cristales según las condiciones delim entorno.
Después, los equipos analizaron las variables que obtuvieron para establecer los modelos matemáticos que describieran la relación entre ellas y el crecimiento cristalino, así como los patrones formados en las estructuras. Con base en estos análisis, elaboraron diversos gráficos ilustrativos (Figura 4).
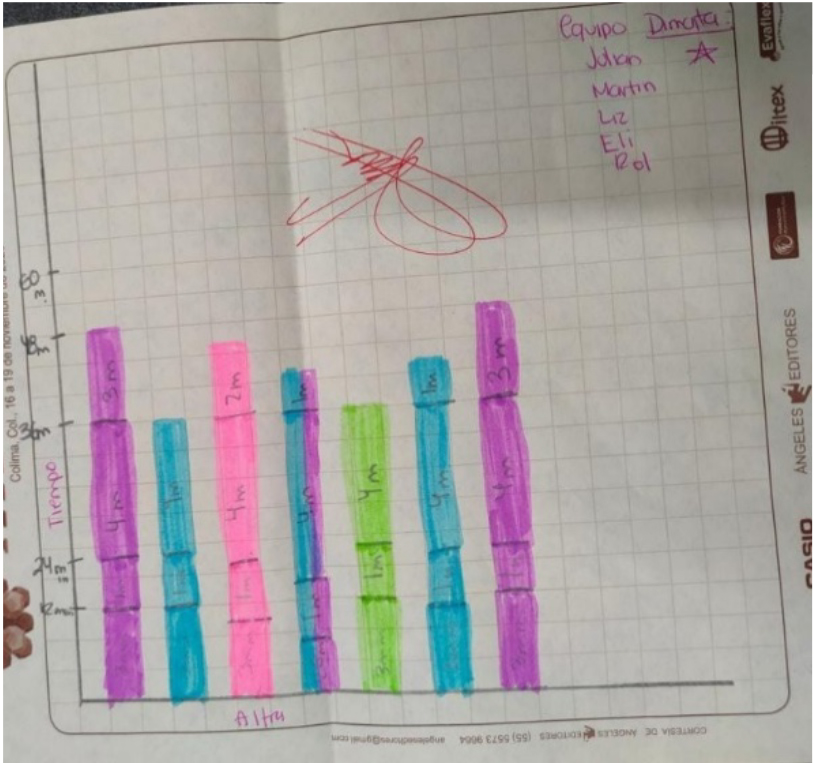
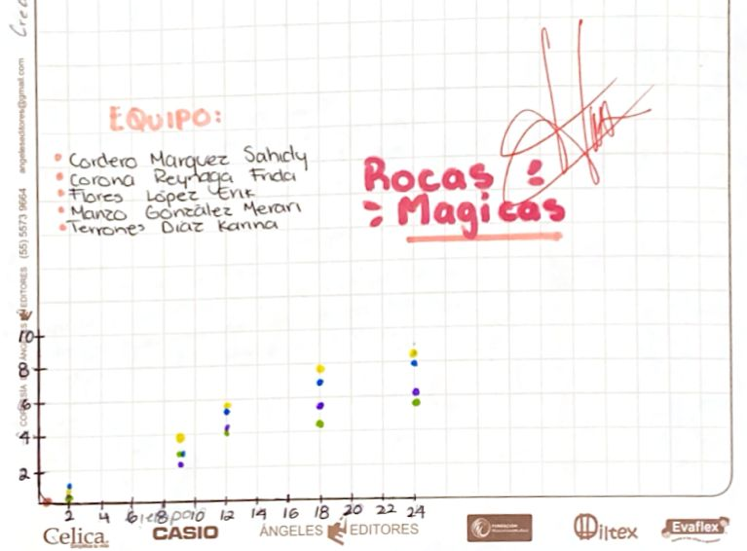
Figura 4. Registros de información.
Para darle un sentido matemático al experimento, los alumnos debieron estipular las variables a considerar:
Variable independiente: es aquella que puede ser manipulada o controlada por los estudiantes durante el experiment; por ejemplo, el tiempo trascurrido o la temperatura del agua.
Variable dependiente: corresponde al resultado que se observa y mide a lo largo del experimento, en este contexto, el tamaño o la altura alcanzados por los cristales.
A fin de orientar al estudiantado en el análisis matemático del experimento, se pueden plantear preguntas que les permitan reflexionar sobre los elementos involucrados. Por ejemplo, ¿qué sucede si se aumenta o disminuye la temperatura inicial del agua?, ¿cómo influye el tiempo de exposición en la formación de los cristales?, ¿se pueden establecer patrones de crecimiento con base en los datos recopilados?, ¿el crecimiento de los cristales sigue una tendencia lineal o no lineal?
Una vez determinadas las variables, cada equipo organizó sus mediciones en una tabla donde registraron el tiempo transcurrido y la altura de cada cristal. Con tal información, se procedió a trazar gráficamente los datos, empleando un software como GeoGebra o Excel para el modelado matemático. Estos programas hicieron posible ajustar los datos del experimento, contrastar diversos modelos, comparar ecuaciones representantes del crecimiento de los cristales y ajustar los parámetros para obtener una representación fiel del fenómeno.
A partir del uso de graficadores, los estudiantes pueden visualizar los datos y determinar la composición del modelado; si el comportamiento es lineal, adopta la forma y = mx + b; si se observa una relación exponencial, puede ajustarse con una expresión del tipo y = aebx.
Después del planteamiento del modelo, se procedió a cotejarlo con los datos del experimento y verificar su grado de ajuste. Esta comparación consideró todos los cristales formados en cada tanque, que contenía cinco o seis rocas. En esta fase, los equipos debían relacionar el ejercicio práctico con los conocimientos teóricos y formular conjeturas basadas en la observación, como las siguientes:
Ocurren procesos similares en la formación natural de estalagmitas y estalactitas en cuevas como resultado del goteo de agua rica en minerales.
Los depósitos salinos en zonas desérticas se forman porque la evaporación de lagos salados deja atrás cristales de sal acumulados.
Ejemplos como estos albergan comparaciones con fenómenos naturales generados en el entorno y facilitan formular hipótesis sobre las variables que son favorables para un crecimiento más acelerado o con una mayor solidez en los cristales. Esta etapa del experimento invita a una discusión en distintos ejes temáticos, como el patrón geométrico y la simetría de las estructuras cristalinas. Por último, el fenómeno de estudio puede modelarse a partir de ecuaciones, tales como el crecimiento cristalino en función del tiempo o las relaciones de proporcionalidad entre la cantidad del soluto y la formación de estructuras cristalinas.
La modelación matemática se ha consolidado como una herramienta pedagógica de gran valor en todos los niveles educativos; desde la formación básica, donde introduce elementos de interpretación, hasta la superior, donde abre camino a la experimentación con problemas típicos de la ingeniería y la construcción. Su utilidad no se limita al aprendizaje de las matemáticas, ya que también brinda a los estudiantes la posibilidad de comprender conceptos abstractos y, en especial, aplicarlos a situaciones del mundo real. Esta capacidad de vincular teoría y praxis es lo que la convierte en una estrategia didáctica valiosa.
La enseñanza tradicional de las matemáticas suele centrarse en la memorización de fórmulas y la resolución de problemas tipo, lo que a menudo genera una desconexión entre el estudiante y la aplicabilidad real del conocimiento adquirido. Esta clase de educación ha sido superada por perspectivas más integrales, como la que propone la Nueva Escuela Mexicana, donde las matemáticas se entienden como una herramienta viable en diversos contextos cotidianos.
Faulkner et al. (2019) destacan que, al modelar situaciones del mundo real a través de las matemáticas —sin importar el área de estudio—, los alumnos desarrollan habilidades analíticas y de pensamiento crítico, esenciales para resolver problemas complejos y prácticos. Tal capacidad, además de fortalecer su proceso formativo, también contribuye a que reconozcan la relevancia de las matemáticas en su vida cotidiana y su crecimiento profesional. La verdadera importancia de la modelación matemática reside en la capacidad de vincular la teoría con la práctica, de manera que la comunidad estudiantil adquiera consciencia de cómo las matemáticas inciden en múltiples campos del conocimiento.
Bajo el enfoque STEM (ciencia, tecnología, ingeniería y matemáticas), como fue en el experimento realizado por los estudiantes de la LEM, el modelado se consolida como una herramienta que promueve una amplia gama de habilidades. A la vez que les ayuda a preparar recursos aplicables para su futura labor docente, también impulsa el pensamiento crítico y la reflexión sobre su desempeño profesional.
Como lo advierte Pollak (2007), enseñar no se limita a la trasmisión de conocimientos mediante un discurso; implica motivar a la comunidad escolar a, desde el interés propio, plantear situaciones, explorar problemáticas y construir escenarios que faciliten tanto la interpretación matemática como la comunicación efectiva de ideas. Dicho enfoque considera la comprensión de las matemáticas y también fortalece la habilidad para aplicarlas en contextos prácticos.
En esta línea, el modelado matemático debe considerarse una habilidad esencial en la formación docente, ya que permite a maestros y estudiantes explorar y resolver problemas auténticos. Dentro de este contexto educativo actual donde se valoran las habilidades prácticas y transferibles, la capacidad de modelar situaciones reales mediante las matemáticas se vuelve imprescindible. Asimismo, la instrucción de futuros docentes se enfoca en la enseñanza de las matemáticas de forma comprensible y aplicable, superando los métodos basados en la memorización de conceptos. Bajo esta premisa, se reconoce que el modelado matemático contribuye a generar experiencias de aprendizaje significativo.
Las demandas educativas actuales subrayan la necesidad de una formación interdisciplinaria en los docentes. En este sentido, es menester que los profesores de matemáticas adquieran la capacidad de indagar en procesos químicos, biológicos y físicos, con el fin implementar modelos que integren diversas áreas y respondan a contextos reales y complejos. Incorporar la modelación matemática en el currículo promueve una educación más completa y versátil, donde los estudiantes pueden reconocer la aplicabilidad de las matemáticas en su vida cotidiana y en su rendimiento profesional. Del mismo modo, esta práctica fomenta el desarrollo de habilidades críticas y analíticas para enfrentar un mundo cada vez más complejo y atravesado por la tecnología.
Blum, W. (2015). Quality Teaching of Mathematical Modelling: What Do We Know, What Can We Do? En S. J. Cho (Ed.), The Proceedings of the 12th International Congress on Mathematical Education (pp. 73–96). Springer.
Blum, W. y Borromeo, R.(2009). Mathematical Modelling: Can It Be Taught And Learnt? Journal of Mathematical Modelling and Application, 1(1), 45–58.
Blum, W. y Leiß, D. (2007). How do Students and Teachers Deal with Modelling Mathematical Problems? En C. Haines, P. Galbraith, W. Blum y S. Khan (Eds.), Mathematical Modelling. Education, Engineering and Economics—ICTMA 12 (pp. 222–231). https://doi.org/10.1533/9780857099419.5.221
Blum, W. y Niss, M. (1991). Applied mathematical problem solving, modelling, applications, and links to other subjects — State, trends and issues in mathematics instruction. Educational Studies in Mathematics, 22, 37–68. https://doi.org/10.1007/BF00302716
Blum, W., Galbraith, P. L., Henn, H. W. y Niss, M. (Eds.) (2007). Modelling and Applications. Springer.
Borromeo, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. ZDM – Mathematics Education, 38, 86–95. https://doi.org/10.1007/BF02655883
Faulkner, B., Earl, K. y Herman, G. (2019). Mathematical Maturity for Engineering Students. International Journal of Research in Undergraduate Mathematics Education, 5, 97–128. https://doi.org/10.1007/s40753-019-00083-8
Greefrath, G. y Vorhölter, K. (2016). Teaching and Learning Mathematical Modelling: Approaches and Developments from German Speaking Countries. Springer. https://doi.org/10.1007/978-3-319-45004-9_1
Guerrero, L. y Terrones, D. (2003). Repertorio de estrategias pedagógicas. PROMEB-Piura.
Kaiser, G. y Schwarz, B. (2006). Mathematical modelling as bridge between school and university. ZDM – Mathematics Education, 38, 196–208. https://doi.org/10.1007/BF02655889
Kaiser, G. y Stender, P. (2013). Complex Modelling Problems in Co-operative, Self-Directed Learning Environments. En G. Stillman, G. Kaiser, W. Blum y J. Brown (Eds.) Teaching Mathematical Modelling: Connecting to Research and Practice (pp. 277–293). Springer. https://doi.org/10.1007/978-94-007-6540-5_23
Lesh, R. y Doerr, H. M. (Eds.) (2003). Beyond constructivism: models and modeling perspectives on mathematics problem solving, learning, and teaching. Lawrence Erlbaum Associates Publishers.
Maass, K. y Engeln, K. (2018). Impact of professional development involving modelling on teachers and their teaching. ZDM – Mathematics Education, 50, 273–285. https://doi.org/10.1007/s11858-018-0911-y
Pollak, H. (1977). The interaction between mathematics and other school subjects (including integrated courses). En H. Athen y H. Kunle (Eds.), Proceedings of the Third International Congress on Mathematical Education (pp. 255–264).
Pollak, H. (2007). Mathematical Modelling — a Conversation with Henry Pollak. En W. Blum, P. L. Galbraith, H. W. Henn, y M. Niss (Eds.), Modelling and Applications in Mathematics Education (pp. 109–120). Springer.
Santana Ortega, A., Gómez Blancarte, A. L. y López López, O. N. (2018). Experimentación, modelación y simulación matemática en la formación de profesoras de telesecundaria. Congreso Nacional de Investigación sobre Educación Normal. https://es.scribd.com/document/649174665/P042Universidad
Universidad de Colima (2015). Licenciatura en Enseñanza de las Matemáticas. Documento curricular. Versión impresa. México.