![]() Jesús Eduardo Hinojos Ramos1,2
Jesús Eduardo Hinojos Ramos1,2
1 Universidad Autónoma de Querétaro, Querétaro, México
2 Instituto Tecnológico de Sonora, Sonora, México
Recibido el 26 de enero de 2024, aceptado el 24 de septiembre de 2024.
La presente investigación se propone determinar las habilidades de pensamiento abstracto lógico (HPAL) desarrolladas por alumnos de educación superior; para alcanzar esa meta, se creóun software enfocado en la simulación de circuitos eléctricos compatible con los procesos de aprendizaje de nivel universitario, con el fin de caracterizar acciones cognitivas y metacognitivas exhibidas por los participantes al operarlo. En ese sentido, se usan métodos constructivos demodelización matemática dinámica en el ámbito de la metacognición desde una perspectiva de linealización (MDL). La ventaja de este diseñoinfraestructural yace en que la interfaz constituye una opción asequible y versátil, porque se ha programado en lenguaje C# de código abierto, ya sea para ejecutarse en la red o bien instalarse desde sistemas operativos convencionales. El trabajo desempeñado por los estudiantes durante las pruebas preliminares fue satisfactorio. Seles presentó una novedosa interfaz de usuario instalable en Windows o accesible vía navegadores web. Los resultados permitieron evaluar el progreso de las habilidades del pensamiento y generar métodos y estrategias de enseñanza-aprendizaje. Así, su análisis, argumentación e interpretación de los circuitos eléctricos constituyen un aporte significativo para la docencia en general y la matemática educativa en particular..
Palabras clave: didáctica de las ciencias, habilidades de pensamiento abstracto lógico, metacognición desde una perspectiva de linealización, modelos matemáticos, secuencia didáctica, software didáctico.
This research work focuses on characterizing the abstract logical thinking skills (ALTS) developed by college students; to that end, an electrical circuits simulation software compatible with the learning processes of university students was created; moreover, the cognitive and metacognitive actions exhibited by the participants when operating it were characterized. Dynamic mathematical constructive modeling techniques are employed in the field of metacognition from a perspective of linearization (MPL). An advantage of such an infrastructure design is that the interface deployed is considered affordable and versatile, since it is programmed in open source language (C#) to be used online or installed on conventional operating systems, such as WinX64. The students' performance during the preliminary tests was satisfactory. They were presented with a novel user interface installable on Windows or accessible via web browser. The results made it possible to evaluate the development of thinking skills and to establish teaching-learning methods and strategies. Their analysis, argumentation and interpretation constitute a significant contribution to teaching in general and to educational mathematics in particular.
Keywords: science didactics, abstract logical thinking skills, metacognition from a linearization perspective, mathematical models, didactic sequence, didactic software.
Las tecnologías de la información y comunicación posibilitan el intercambio entre docentes y estudiantes, propiciando el fortalecimiento de habilidades y competencias disciplinares dentro de varias áreas del conocimiento (Stošić et al. , 2020; Ergashev et al. , 2021). A lo largo de la década de 2010, internet se ha expandido de forma exponencial (Sulakono et al., 2020; Ejiyi et al., 2021) y predominan las aplicaciones y los sistemas digitales en el mercado (Xu et al., 2020; Marakana et al., 2021). Por tanto, se requiere que los profesionales de la educación se pongan a la vanguardia de los procesos de aprendizaje de las ciencias. Asimismo, es necesario definir estrategias de enseñanza precisas, como el establecimiento de mecanismos de información pública a distancia, en concordancia con las recomendaciones de la UNESCO (2022). Los proyectos de aprendizaje efectivos y flexibles deben ponerse en marcha, tanto dentro como fuera de línea, en temas específicos del dominio disciplinar del docente según sus objetivos educativos definidos (Duarte et al., 2021; Sansolis y Leonoras, 2021).
Por otra parte, realizar simulaciones de circuitos eléctricos a través de secuencias didácticas beneficia a los estudiantes que cursan materias de ingeniería como Electromecánica, Electrónica o Control, pues nutre las habilidades técnicas y pragmáticas, y ensancha el conocimiento referente a sistemas eléctricos y electrónicos. No obstante, para que el conocimiento trascienda el dominio teórico es necesario que el estudiante interactúe con el equipo de laboratorio tanto en software como en hardware. De tal modo, adquirirá destreza para poder aplicarlas en situaciones prácticas, relacionando los conceptos abstractos con circunstancias del mundo real, incluyendo el análisis e interpretación de secuencias lógicas y didácticas (Coughlan, 2020).
En palabras de Lee y Lee (2021), las aplicaciones en móviles y ordenadores para la educación de las ciencias exactas ofrecen oportunidades de enseñanza y aprendizaje adaptables a los requisitos pedagógicos. Los trabajos de Sansolis y Leonoras (2021) se centran en las habilidades desarrolladas por los estudiantes mediante las tecnologías de información (TI); en su investigación encontraron, por lo menos, 15 diferencias significativas en aspectos psicométricos y cognitivos a través de secuencias didácticas enfocadas en el aprendizaje de las modelizaciones matemáticas. En trabajos de Ejiyi et al. (2021) diseñaron una aplicación escolar que mejora los procesos de aprendizaje y de planificación, con el fin de compararla con las alternativas comerciales; como apps enfocadas en la metacognición, en virtud de mejorar los procesos de aprendizaje y planificación escolar de los alumnos. Algunas indagaciones, como las de Akmar et al. (2021) y de Bakar et al. (2021), proponen la generación de interfaces flexibles para desarrollar habilidades en los procesos de aprendizaje en campos de la ciencia y la tecnología, como es el caso de la ingeniería matemática de la modelización.
De esta manera, hay trabajos enfocados en los métodos de modelado matemático de solución de circuitos RLC (resistor, inductor y capacitor). Las leyes de Kirchhoff sustentan la modelización de circuitos equivalentes por medio de programación no-lineal para estimar parámetros de tensión y corriente en el dominio de Laplace (Bocanegra et al.., 2020). En paralelo, técnicas como la de Astorga (2014) trazan la representación gráfica de las armónicas de tensión y corriente utilizando el modelado de la función de transferencia entre los datos originales y el valor teórico obtenido a partir de la función no lineal considerada (Fiallos, 2021).
El aprendizaje basado en modelizaciones matemáticas posibilita precisar el comportamiento de un sistema real eligiendo diferentes alternativas de diseño, como los modelos de regresión lineal para sistemas de primer orden (RL), o la múltiple en sistemas eléctricos, entre ellos los lineales y exponenciales (RLC) (Gu, 2011; Papa, 2017; T Widiharih, 2021); asimismo, han sido de utilidad en sistemas dinámicos para describir la evolución de dichos sistemas en su función del periodo de tiempo (Dijkstra y Henseler, 2021; Ren et al., 2021). A todo esto, la respuesta tentativa a la pregunta de investigación es que, en comparación con una enseñanza tradicional, los estudiantes de ingeniería logran una comprensión más acertada del modelado matemático a partir de la aplicación de una infraestructura experimental diseñada específicamente para ese fin.
En lo subsecuente, se propone la creación de una infraestructura experimental accesible para la modelación matemática de circuitos eléctricos que sirva en los procesos de enseñanza-aprendizaje en la educación de nivel superior. Tal plataforma debe facilitar la identificación y potencialización del desarrollo de habilidades del pensamiento abstracto lógico, como el análisis dinámico del problema real contextualizado en secuencias didácticas.
La presente investigación se basa en cuatro conceptos centrales; el primero es la situación real del problema, donde se diseña y estudia un problema contextualizado referente a las ciencias exactas en una secuencia didáctica. En segunda, el modelo real del problema se enfoca en realizar la representación matemática del sistema acorde a la situación real. En tercera, el modelado matemático del problema radica en la habilidad de formular soluciones a partir del razonamiento y la comparación de las expresiones matemáticas del comportamiento de un sistema mecánico o eléctrico (Kaiser y Brand, 2015). Por último, las acciones cognitivas y metacognitivas en los estudiantes enlistan y evalúan las actividades mentales a partir de las cuales ellos generan estrategias autónomas de aprendizaje; de ese modo es posible observar el equilibrio enseñanza-aprendizaje (Niss, 2017; Niss y Blum, 2020).
Se parte de un modelo que representa matemáticamente el comportamiento del sistema concorde a la situación real del problema a analizar. De acuerdo con Kaiser y Brand (2015), formular y solucionar problemas del mundo real facilita desarrollar nuevas maneras y métodos de simulación que sirven de instrucción a los estudiantes en los procesos de enseñanza-aprendizaje.
La aplicación de estrategias pedagógicas basadas en las HPAL ha sido angular para nutrir la capacidad de los alumnos al resolver problemas cotidianos mediante el modelado matemático. Jaramillo y Peña (2016) apuntalan que el ciclo de la construcción y reconstrucción del conocimiento se orienta a las destrezas y los procesos cognitivos que constituyen el pensamiento lógico abstracto por medio de actividades académicas donde se evalúan las aptitudes. Bajo esta perspectiva, la medida del pensamiento abstracto con que se llevan a cabo las destrezas cognitivas de síntesis, deducción, asociación e interpretación de fenómenos (Tolan et al., 2021). En paralelo, los procesos cognitivos como relacionar, evaluar, deducir, identificar e inferir en tareas diarias son estrategias que permiten estimular un aprendizaje significativo en los estudiantes (Akpur, 2021).
La modelación es una estrategia de formulación y diseño de algoritmos matemáticos enfocados en comprender a profundidad lo que ocurre en un sistema (Bossio et al., 2023). Asimismo, su práctica amplía la percepción y facilita la transferencia de habilidades elementales hacia los alumnos (Fonseca, 2023). En el marco institucional, tal estrategia admite acciones realistas y abiertas, y otorga una metodología para que los profesores conciban cómo aplican los alumnos el pensamiento crítico en la solución de problemas (Marbouti y Strobel, 2013).
Los procesos transitorios de primer y segundo orden de circuitos eléctricos son cognoscibles a partir de ecuaciones diferenciales en el dominio del tiempo (Bueno Hernández et al., 2020). Los modelos no-lineales describen el comportamiento e incluso estiman la evolución de un sistema real en un periodo de tiempo, y para lo cual existen varias alternativas de diseño (Dijkstra y Henseler, 2021; Ren et al., 2021). En suma, las concepciones del proceso de modelado matemático (MM) integradas en secuencias didácticas ayudan a consolidar el conocimiento disciplinar en circuitos eléctricos (CDCE) (Recio, 2018; Bravo y Rodríguez, 2020). Se dice que un modelado matemático está bien estructurado cuando los alumnos realizan el desglose de un sistema real siguiendo una secuencia didáctica. Esbozan una resolución impresa a lápiz y papel (RILP), a partir de la cual reciben una retroalimentación al instante que tiene por base la solución del modelado propuesto (SMP) en cada etapa del ciclo de modelado: diseño, modelación e implementación (Abassian et al., 2020).
Se propone un estudio cualitativo basado en dos estrategias: la primera utiliza, a lo largo de una secuencia didáctica, una infraestructura experimental ligada a la enseñanza de las ciencias exactas para el modelado matemático; la segunda continúa con el método tradicional para la solución de secuencias didácticas. Ambas modalidades usan los métodos constructivos de modelización que conceden realizar una intervención didáctica regida por el dominio de la teoría hpal. La presente está perfilada a académicos de las ciencias exactas interesados en identificar las hpal de sus educandos, con el fin de generar estrategias pedagógicas de naturaleza cognitiva, a través de la modelización y el análisis dinámico de problemas reales contextualizados.
Para este propósito, se contemplaron cuatro sesiones de 60 minutos (por secuencia), donde participaron voluntariamente cuatro alumnos, uno por cada módulo. La actividad fue organizada en un escenario de construcción social orientado a la modelización y el análisis dinámico desde una perspectiva de linealización (MDL) en circuitos eléctricos de primer y segundo orden. La finalidad fue comparar el proceso educativo del conocimiento disciplinar matemático en la interfaz de usuario en oposición a la enseñanza tradicional en términos de las hpal exhibidas por los voluntarios.
En la gestión y el registro de datos se consideraron dos cartas: la primera, dirigida a los participantes, concierne a la confidencialidad e indica los tiempos y las sesiones a realizar; la segunda atañe al consentimiento informado, donde los participantes proporcionaron su información personal y declararon a consciencia su disposición a involucrarse en el experimento. Para el caso de la infraestructura experimental (interfaz) la información se almacenó al final de cada secuencia de manera automática; en cambio, para el método tradicional fueron los participantes quienes realizaron los registros.
Se adoptaron tanto las técnicas de investigación cualitativa descritas por Del Río (2011) y Sánchez et al. (2022), como el análisis de contenido cualitativo de los estudios de marcos de codificación y modelado de Lu y Kaiser (2021). Ambos se operacionalizaron para determinar las acciones y los procesos llevados a cabo por los estudiantes por medio de instrumentos de recolección y análisis de datos (Tabla 1.) El primero es la interfaz de usuario referida en la Introducción; programada en lenguaje C-Sharp (C#), sirve para crear secuencias didácticas, que contienen modelaciones matemáticas orientadas por la teoría hpal. De igual manera, se incluye una guía de observación como instrumento para la categoría actitudinal (A) bajo el formato de secuencia didáctica basada en las hpal; se focaliza en procesos cognitivos como la relación, la evaluación, la inferencia y la deducción en las tareas de aprendizaje durante la construcción y reconstrucción del conocimiento.
La categoría procedimental (P) refiere a las habilidades y los procesos cognitivos para formular y ejecutar una modelación matemática mediante la abstracción y el uso de herramientas matemáticas. Se evalúa por medio de una lista de cotejo en dos fases: diseño para el medolado y contenido matemático, e implementación y análisis de resultados para la resolución de la situación de un problema real. Por último, los logros de aprendizajen se determinan mediante un cuestionario de la categoría conceptual (C); se valora el tratamiento y la captura de datos con ayuda de un procesador de textos de licencia libre integrado en la interfaz de usuario.
Tabla 1. Instrumentos para la toma de datos. Fuente: elaboración propia.
| Categoría | Instrumento | Descripción | Justificación |
|---|---|---|---|
|
Actitudinal (A) |
Guía de observación |
Se emplea para obtener información sobre una actividad o fenómeno. |
Funge como una herramienta efectiva para la implementación de secuencias didácticas. |
|
Procedimental (P) |
Lista de cotejo |
Identifica las habilidades a evaluar en el proceso de aprendizaje. |
Define los indicadores y los procesos clave del aprendizaje proyectado. |
|
Conceptual (C) |
Cuestionario |
Son pruebas de validación que consisten en una serie de preguntas específicas |
Establece los logros de aprendizaje, los criterios de evaluación y los niveles de satisfacción. |
C-Sharp (C#) es un lenguaje orientado a objetos que combina las mejores características de sus predecesores, como Java, JavaScript, Visual, Visual Basic o C++. Su compilador, Visual Studio, incluye .net framework sdk (offline con kit de desarrollo de software) y asp.net (paquetes de servicios activos online). Para el soporte del software fue empleado Moodle LMS (sistema de código abierto dedicado a la gestión del aprendizaje) y el motor SQL Server Management Studio 18.0, con el cual se montó una base de datos en línea. Asimismo, el script, que contiene un código estructurado del software, puede correr en una página web o instalarse en sistemas operativos Windows o Mac como indica la norma ISO/IEC/IEEE 24774:2021. Aspectos del sistema tales como la arquitectura de la interfaz, el procedimiento y la representación matemática son indispensables al crear secuencias didácticas para el modelado del problema contextualizado a analizar mediante las acciones metacognitivas.
La comunicación simultánea entre el software Simulink (extensión de MathWorks MATLAB) y el hardware Arduino Nano se logró mediante la paquetería ArduinoI/O; este arreglo en C# constituye la interfaz de usuario para la modelación matemática (Figura 1). En suma, la adquisición de datos, su procesamiento y la devolución de resultados se organizan en tres bloques:
- Adquisición: Pone su atenición en la recepción de datos, tales como variables dependientes e independientes, escalón unitario, resistencia (R), inductor (L) y capacitor (C).
- Procesamiento: Determina la función de transferencia de salida, las armónicas en procesos transitorios de circuitos eléctricos RLC en el dominio del tiempo, la frecuencia natural ( fn) y el coeficiente de amortiguamiento ( δ). Para ello, se desarrolla un modelado dinámico desde una perspectiva de linealización (MDL), aplicando la transformada de Laplace para el circuito a partir de ecuaciones diferenciales (Kú et al., 2008).
- Resultados numéricos y gráficos: Expone los valores del modelado, el AQfactor de amortiguamiento ( δ), la frecuencia natural ( fn) y la respuesta de simulación.
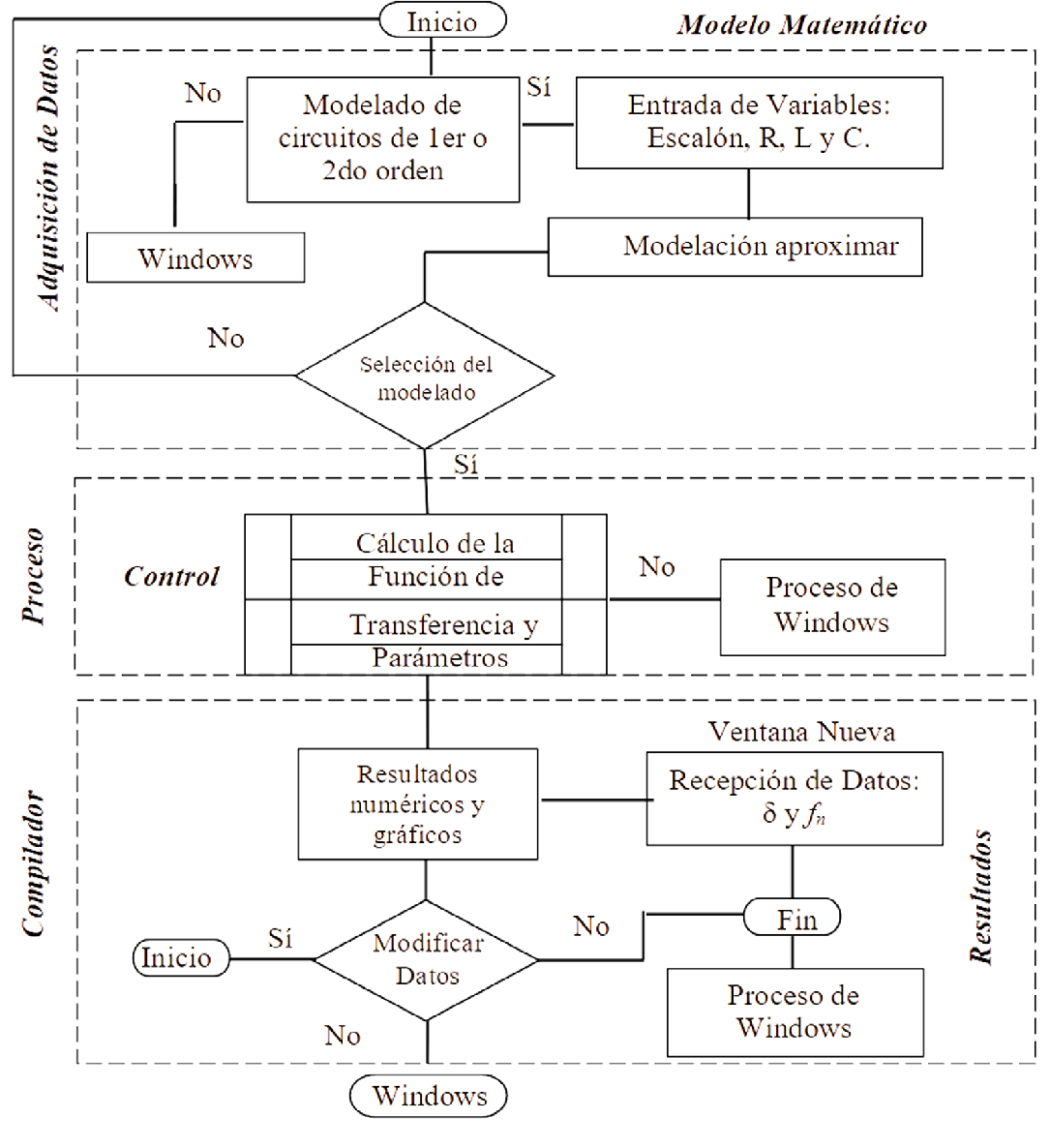
Figura 1. Bloques de la secuencia de flujo para una modelización matemática.
El proceso se realiza dentro de la interfaz y consiste en estructurar dos secuencias didácticas mediante modelizaciones matemáticas de un problema real con enfoque en la enseñanza-aprendizaje.
Primera secuencia didáctica. Examinar el comportamiento de la función de transferencia de salida y de las armónicas de circuitos eléctricos en el domino del tiempo, en procedimientos transitorios de circuitos eléctricos rlc (resistor, inductor y capacitor) de segundo orden (Tabla 2).
Actividad 1. Implementar de manera experimental un circuito eléctrico de segundo orden compuesto por un resistor, un inductor y un capacitor. Del mismo modo, en el circuito, la resistencia y el inductor se conectarán en serie, mientras que el capacitor se acoplará en paralelo (Figura 2).
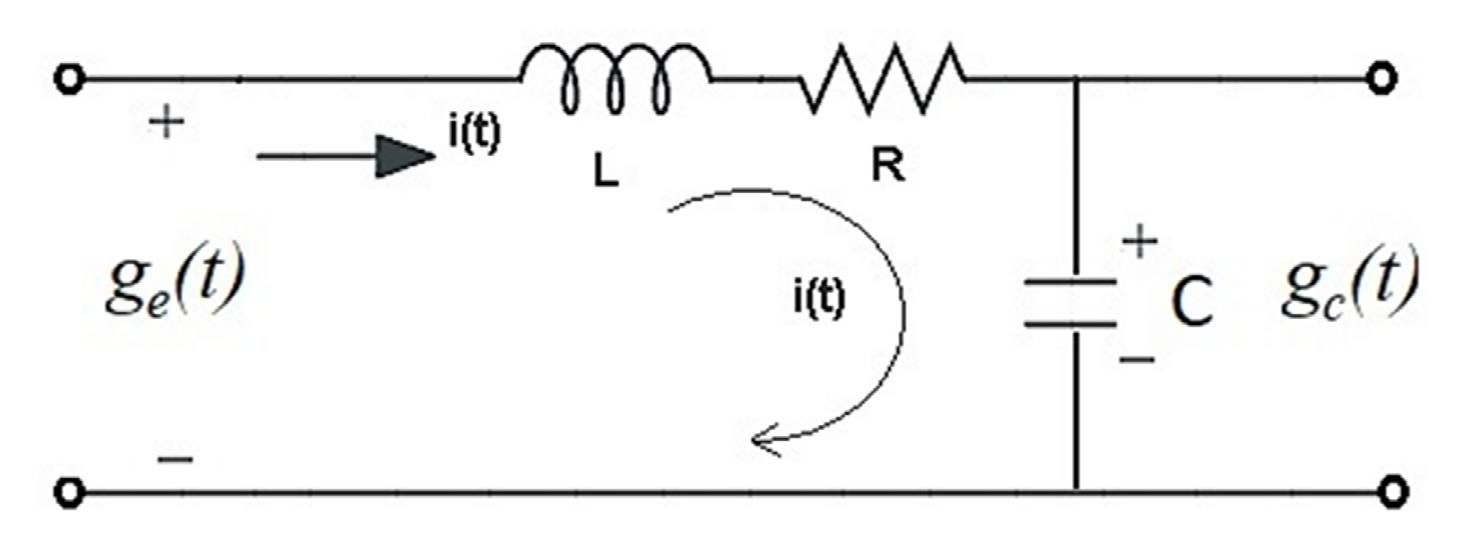
Figura 2. Circuito RLC de segundo orden.
Modelado. Realizar la modelización del circuito RLC mediante ecuaciones diferenciales basadas en la ley de voltajes de Kirchhoff para un circuito de segundo orden.
Las variables consideradas son: resistor (R), inductor (L), capacitor (C), voltaje de entrada ge (t) y voltaje de salida en el capacitor gc (t).
Tabla 2. Primera secuencia didáctica. Fuente: elaboración propia.
| Resolución impresa a lápiz y papel | Resolución ante la interfaz (guía) |
|---|---|
|
Pregunta 1. Determina la caída de voltaje para el circuito eléctrico de segundo orden rlc. |
Resolución 1. La caída de voltaje alrededor de un lazo cerrado
debe ser igual a cero.
|
|
Pregunta 2. Transforma la ecuación obtenida al dominio de Laplace. |
Resolución 2. La Ecuación (1) convertida al dominio de Laplace es: |
|
Pregunta 3. Calcula la corriente de entrada en dominio de frecuencia. |
Resolución 3. Al despejar de la Ecuación (2) la corriente de entrada I(s) resulta: |
|
Pregunta 4. Obtén el voltaje en la salida del capacitor en el dominio del tiempo. |
Resolución 4. Por tanto, el voltaje de salida del capacitor es igual a:
|
|
Pregunta 5. Aplica en el capacitor la transformada de Laplace al voltaje de salida. |
Resolución 5. Al transformar a frecuencia y despejar
la corriente I(s) se tiene:
|
|
Pregunta 6. Encuentra la razón del voltaje de entrada con respecto al de salida. |
Resolución 6. La razón del voltaje de entrada con respecto
al voltaje de salida se calcula con:
|
|
Pregunta 7. Define la función de transferencia F(s). |
Resolución 7. La función de transferencia F(s) sería:
|
|
Pregunta 8. Determina la función de transferencia que incluye los parámetros de frecuencia natural (fn) y el factor de amortiguamiento (δ) del circuito eléctrico. |
Resolución 8. La transferencia en función de la frecuencia natural (fn)
y el factor de amortiguamiento (δ) del rlc es:
|
|
Pregunta 9. Calcula los parámetros del circuito eléctrico de acuerdo con las siguientes expresiones. |
Resolución 9. Para calcular los parámetros del circuito eléctrico
se usan las siguientes expresiones:
|
|
Pregunta 10. Determina la respuesta de un circuito de segundo orden en el dominio del tiempo ante un escalón unitario. |
Resolución 10. La respuesta de un circuito de segundo orden en el dominio del tiempo ante un escalón unitario. |
Segunda secuencia didáctica. Analizar el comportamiento de la corriente en función del tiempo i(t) dentro de un circuito rl conectado en serie (Tabla 3).
Actividad 2. Analizar el comportamiento del término transitorio en la función i(t) a partir de la armónica generada por el circuito de primer orden, e identificar los valores de la resistencia y el inductor (Figura 3)
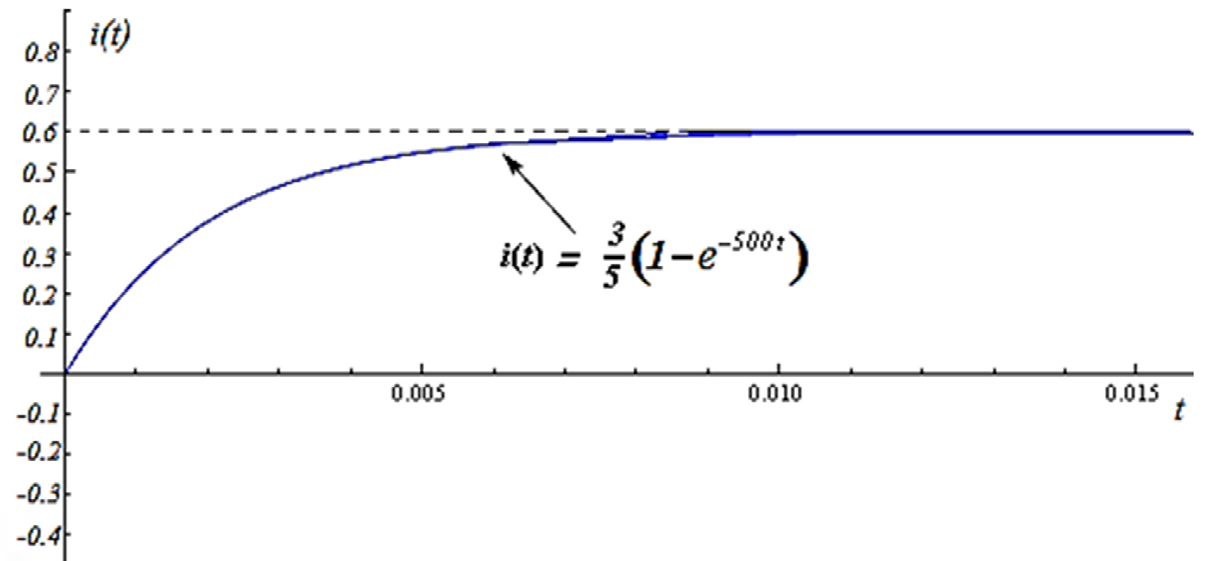
Figura 3. Circuito eléctrico de primer orden, tipo RL.
Modelado. Modelar los parámetros a raíz de la armónica del RL mediante ecuaciones diferenciales. Las variables son: R, L, voltaje de entrada E(t) y voltaje de salida en el inductor gl(t).
Tabla 3. Segunda secuencia didáctica. Fuente: elaboración propia.
| Resolución impresa a lápiz y papel | Resolución ante la interfaz (guía) |
|---|---|
|
Propuesta 1. Desglosar el comportamiento de la armónica de la función de la corriente. |
Propuesta 1. Desglosar el comportamiento
de la armónica de la función de la corriente.
|
|
Proceso 1. Fase de diseño. Proceso de modelación atemática, así como del contenido matemático. |
Proceso 1. Para la fase de diseño, se parte de la armónica de la Figura 3. Su función general se compone de dos soluciones: Asimismo, el circuito de primer orden rl en serie tiene la forma: |
|
Proceso 2. Fase de implementación y análisis de resultados. Lo conforman la implementación del diseño y la resolución de la situación-problema para una modelación matemática. |
Proceso 2. Fase de implementación y análisis de resultados. Los ejes coordenados en el dominio del tiempo son t para las abscisas e i(t) para las ordenadas; es decir, la armónica se extiende desde (0,0) hasta (∞, i(t)). Si cuando t → ∞ ,
|
Una vez diseñadas las secuencias en la interfaz, se implementan con estudiantes, a fin de fomentar un proceso de aprendizaje. El experimento consistió en la realización de prácticas divididas en seis fases:
1) Introducción al manejo de componentes eléctricos y hardware. Conexión y simulación de circuitos eléctricos de primer y segundo orden aplicando las leyes de Kirchhoff en la modelización de arreglos RL, RC y RLC.
2) Repaso del modelado mediante software. Los temas abordados fueron las funciones de transferencia entrada-salida en circuitos eléctricos, el comportamiento del voltaje y la corriente, las constantes de tiempo y las respuestas de sistemas de primer y segundo orden.
3) Modelado de la función de transferencia. Identificación de la respuesta de circuitos eléctricos para sistemas de primer (RL o RC) y segundo orden (RLC), configuración de hardware, software, así como la validación del modelo en el dominio del tiempo.
4) Interpretación de resultados. Se estudiaron los gráficos de la modelización del comportamiento del RLC en el dominio del tiempo ante el estímulo de un escalón unitario.
5) Comunicación de la interfaz de usuario. Se realiza a través de Simulink de Matlab mediante una tarjeta de control.
6) Conexión directa entre el software (la interfaz experimental) y el hardware (los componentes eléctricos y la tarjeta de control). Se entabla de formas física y simulada.
Las prácticas fueron desarrolladas de forma mixta: se realizaron de forma virtual la introducción, el manejo y el diseño de la plataforma; se llevó a cabo en modo presencial el ensamble, las conexiones y la implementación física. En las etapas físicas los estudiantes usaron capacitores, resistencias e inductores de diferentes denominaciones en el diseño de circuitos de segundo orden; así, fueron capaces de generar los tres tipos de respuesta: sistema amortiguado, críticamente amortiguado y sobre amortiguado.
Con base en una de las propuestas de diseño RL (Figura 4) y los datos proporcionados, los estudiantes consiguieron desglosar el comportamiento del circuito (Figura 4A). Para resolver el sistema (Figura 3), algunos optaron por aplicar ecuaciones diferenciales a una ecuación lineal homogénea estándar (Figura B), en lugar de recurrir al método de Laplace ejecutado por la plataforma experimental. Al final del modelado, lograron identificar el término transitorio que forma parte del comportamiento de la función de corriente; dedujeron que, cuando t tiende a infinito, la corriente se fija en 3/5; en otras palabras, la armónica se estabiliza (Figura 4C).s
|
|
|
|
A) Desglose del comportamiento del circuito rl. | B) Forma estándar de la ecuación lineal homogénea. | C) Comportamiento de la función de corriente i(t). |
|---|
Figura 4. Modelado del comportamiento de la función de corriente i(t) de un circuito RL.
En lo que respecta a la relación con las acciones cognitivas para la generación de estrategias de enseñanza-aprendizaje y con base en los análisis de ambas secuencias didácticas, los datos del desempeño de los alumnos se organizaron dentro de tres modalidades. La nomenclatura se desglosa como sigue: SMP (solución del modelado propuesto), RMI (resolución mediante la interfaz), RILP (resolución impresa a lápiz y papel). Puede apreciarse que los participantes tuvieron mayor dificultad para dilucidar sus respuestas y modelados en el rubro RILP con respecto al SMP (Tabla 4).
Tabla 4. Modalidades registradas bajo ítems en la organización de datos. Fuente: elaboración propia.
Nota: Nomenclatura: B solo responde; A analiza y modela correctamente el problema. Modalidades: solución al modelado propuesto (SMP), resolución mediante la interfaz (RMI), resolución impresa a lápiz y papel (RILP).
El desglose considera los elementos descritos en el marco teórico incluyendo el descriptivo y el restrospectivo. En cuanto a la categoría A, la actividad 1 (Tabla 5) se evaluó en función de la construcción y reconstrucción del conocimiento (A1), el pensamiento abstracto (A2) y los procesos cognitivos (A3).
Tabla 5. Categoría Actitudinal (A): Guía de Observación. Fuente: elaboración propia.
Nota: Nomenclatura: 1, deficiente; 2, regular; 3, eficiente.
En la categoría A, el aspecto A1 mantiene un balance en las tres modalidades registradas (smp, rmi, rilp), a diferencia del A3, que presenta carencias en la modalidad RILP. En el aspecto A2 se observó un desempeño general superior a los aspectos A1 y A3, debido a las habilidades y destrezas propias de la formación académica de los participantes.
Tabla 6. Categoría Conceptual (C): Para el Cuestionario. Fuente: elaboración propia.
Al analizar el cuestionario para la categoría C (Tabla 6), se evaluaron las destrezas del estudiante: la abstracción, es decir la lógica aplicada para diseñar y ejecutar el modelado del sistema; la interpretación, en otras palabras, las acciones tomadas, los procesos desarrollados y la aplicación certera de herramientas y habilidades. Es crucial señalar que los resultados de la segunda destreza están por debajo del estándar con respecto a la primera y que, de las tres modalidades, hay más insuficiencia en los métodos tradicionales RILP, debido a varios factores, entre los que predomina la desconcentración de los participantes.
Tabla 7. Categoría Procedimental (p): Lista de cotejo. Fuente: elaboración propia.
Nota: Nomenclatura para máximos valores permisibles por categoría: 1, deficiente; 2, regular; 3, eficiente. Sistema real desglosa-do (SRD), fase de diseño (FD), fase de implementación (FI).
Conviene señalar la categoría P, que contempla la lista de cotejo y la actividad 2 (Tabla 7). Los parámetros a evaluar son la noción de modelación matemática respecto a la situación-problema y los procesos de cognición desarrollados con la modelización matemática. Se toman en consideración las fases de diseño (FD) y de implementación (FI); la modalidad control se denomina sistema real desglosado (SRD). De forma similar, se observó que para los estudiantes existen obstáculos en la primera fase cuando no cuentan con una interfaz de usuario o software, empero, una vez que proceden a la implementación, la dificultad disminuye, potencializando al máximo sus habilidades matemáticas.
La validación funcional de las secuencias didácticas se ejecuta a través de los instrumentos de análisis y recolección de datos en la interfaz de usuario. Tal como indican Vesga y Losada (2018), “se requiere incorporar cambios en los diseños curriculares de los docentes de acuerdo a los fines de la educación matemática”. El presente estudio se basa en la solución a un modelo propuesto (SMP), con el propósito de proveer un desarrollo a nivel de competencia en los estudiantes.
Mentzer et al. (2014), concluyen que el modelado matemático predictivo es esencial para el diseño de secuencias en estudiantes en formación; por ende, concuerdan con Lu y Kaiser (2022) en sus trabajos acerca del modelado matemático basado en las habilidades que despliegan los estudiantes en la resolución de problemas. Por un lado, en los procesos cognitivos, las investigaciones de Hidayat et al. (2018) mostraron que los logros en la metacognición, incluyendo la estrategia cognitiva y la autoevaluación, tienen un impacto positivo en las competencias del análisis y el entendimiento del modelado matemático. A consideración de los procesos cognitivos, se valoró el rendimiento del modelado, involucrando otros componentes, como creatividad y originalidad, con la meta de potencializar las habilidades de pensamiento que pueden desarrollar los pupilos.
El objetivo principal del estudio consistió en determinar los procesos de cognición que pueden desarrollar los estudiantes de educación superior mediante modelizaciones matemáticas conforme a la teoría HPAL. Tras el análisis de sus respuestas al modelado matemático propuesto, se puede afirmar que se cumplió con el objetivo, ya que fue posible categorizar las habilidades del pensamiento generadas en el proceso tanto con el uso de una infraestructura experimental como a través del método tradicional de enseñanza aprendizaje. En específico, se caracterizaron las acciones cognitivas y metacognitivas ejecutadas por los estudiantes con la implementación de una comparativa que permitió identificar y registrar las hpal en el marco de cada modalidad empleada. Según los resultados empíricos, se determinó que los logros en la metacognición en la enseñanza tradicional no superaron el desempeño apoyado por la infraestructura experimental, sobre todo en la fase de diseño e implementación al momento del análisis y entendimiento del modelado matemático de los participantes. La categorización de las actividades de análisis, interpretación y argumentación expuesta por los alumnos en el aula marcaron un aporte significativo a la matemática educativa. Este trabajo exhibe cómo en la educación superior actual, la rápida mutabilidad del conocimiento y el uso generalizado de la tecnología demandan nuevas nociones y métodos vanguardistas para planificar y organizar sesiones en clase; en última instancia, esta modernización educativa se traduce en instruir a los educandos a tomar la iniciativa y proactividad en su formación.
Abassian, A., Safi, F., Bush, S. y Bostic, J. (2020). Five different perspectives on mathematical modeling in mathematics education. Investigations in Mathematics Learning, 12,(1), 53-65. https://doi.org/10.1080/19477503.2019.1595360
Akmar, N., Nadhirah, N., Tasneem, A., Sabrina, I. y Nasuha, F. (2021). Design and development EduPocket A+. Momentum: Physics Education Journal, 5(1), 94-100. https://doi.org/10.21067/mpej.v5i1.5700
Akpur, U. (2021). The Predictive Level of Cognitive and Meta-Cognitive Strategies on Academic Achievement. International Journal of Research in Education and Science, 7(3), 593-607. https://doi.org/10.46328/ijres.1444
Astorga, J. M. (2014). Aplicación de modelos de regresión lineal para determinar las armónicas de tensión y corriente. Ingeniería Energética, 35(3), 234-241. https://dialnet.unirioja.es/servlet/articulo?codigo=5131934
Bakar, Z., Salim, F., Zainuddin, N., Noor, N. y Mohemad, R. (2021). Analysis of Web-based Learning Interface Design based on Experts Verification for Higher Education. JOIV International Journal on Informatics Visualization, 5(2), 134-138. https://doi.org/10.30630/joiv.5.2.410
Bossio, J. L., Santa Ramírez, Z. M. y Jaramillo, C. M. (2023). Un análisis sobre las barreras de la modelación matemática en la práctica educativa del profesor de básica primaria. Revista Virtual Universidad Católica del Norte, (68), 255-285. https://revistavirtual.ucn.edu.co/index.php/RevistaUCN/article/view/1368
Bravo, J. y Rodríguez, L. (2020). Formación del concepto de integral doble mediante la modelación matemática en la carrera de ingeniería informática. Acta Latinoamericana de Matemática Educativa, 33(1), 400-409. https://www.clame.org.mx/documentos/alme33_1.pdf
Bueno Hernández, R., Naveira Carreño, W. y González Hernández, W. (2020). Los conceptos matemáticos y sus definiciones para la formación de los ingenieros informáticos para la sociedad. Universidad y Sociedad. Revista Científica de la Universidad de Cienfuegos, 12(6), 444-452. http://scielo.sld.cu/pdf/rus/v12n6/2218-3620-rus-12-06-444.pdf
Coughlan, T. (2020). The use of open data as a material for learning. Educational Technology Research and Development, 68, 383-411. https://doi.org/10.1007/s11423-019-09706-y
Del Río, O. (2011). El proceso de investigación: etapas y planificación de la investigación. En L. Vilches (Coord.), La investigación en comunicación. Métodos y técnicas en la era digital (pp. 67-96). Gedisa.
Dijkstra, T. y Henseler, J. (2015). Consistent Partial Least Squares Path Modeling. MIS Quarterly, 39(2), 297-316. https://www.jstor.org/stable/26628355
Duarte, D. M., Pedro, L. y Santos, C. (2021). The use of mobile applications in higher education classes: a comparative pilot study of the students' perceptions and real usage. Smart Learning Environments, 8, art. 14. https://doi.org/10.1186/s40561-021-00159-6
Ejiyi, C., Deng, J., Ejiyi, T., Salako, A., Ejiyi, M. y Anomihe, C. (2021). Design and Development of Android Application for Educational Institutes. Journal of Physics: Conference Series, 1769, 1-8. https://iopscience.iop.org/article/10.1088/1742-6596/1769/1/012066/meta
Ergashev, J., Ergasheva, M. y Samatova, G. (2021). Application of Information and Communication Technologies in Solving Geometric Problems. Annals of the Romanian Society for Cell Biology, 25(3), 4191-4197. http://annalsofrscb.ro/index.php/journal/article/view/1909
Fiallos, G. (2021). La Correlación de Pearson y el proceso de regresión por el Método de Mínimos Cuadrados. Ciencia Latina. Revista Multidisciplinar, 5(3), 2491-2509. https://doi.org/10.37811/cl_rcm.v5i3.466
Gu, C. (2011). QLMOR: A Projection-Based Nonlinear Model Order Reduction Approach Using Quadratic-Linear Representation of Nonlinear Systems. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 30(9), 1307-1320. https://doi.org/10.1109/TCAD.2011.2142184
Hidayat, R., Zulnaidi, H. y Syed Zamri, S. (2018). Roles of metacognition and achievement goals in mathematical modeling competency: A structural equation modeling analysis. PLoS one, 13(11), e0206211. https://doi.org/10.1371/journal.pone.0206211
Jaramillo, L. y Puga, L. (2016). El pensamiento lógico-abstracto como sustento para potenciar los procesos cognitivos en la educación. Sophia. Colección de Filosofía de la Educación, (21), 31-55. https://doi.org/10.17163/soph.n21.2016.01
Kaiser, G. y Brand, S. (2015). Modelling competencies: Past development and further perspectives. En G. A. Stillman, W. Blum y M. S. Biembengut (Eds.), Mathematical Modelling in Education Research and Practice. Cultural, Social and Cognitive Influences (pp. 129-149). https://doi.org/10.1007/978-3-319-18272-8_10
Kú, D., Trigueros, M. y Oktaç, A. (2008). Comprensión del concepto de base de un espacio vectorial desde el punto de vista de la teoría APOE. Educación Matemática, 20(2), 65-89. https://www.redalyc.org/pdf/405/40512062004.pdf
Lee, K. y Sim, J. (2021). Design and Development for Mobile Adaptive Layer in Mobile Learning Applications. International Journal of Engineering Research & Technology (IJERT), 10(2), 550-556. https://www.ijert.org/research/design-and-development-for-mobile-adaptive-layer-in-mobile-learning-applications-IJERTV10IS020242.pdf
Lu, X. y Kaiser, G. (2022). Can mathematical modelling work as a creativity-demanding activity? An empirical study in China. ZDM-Mathematics Education, 54, 67-81. https://doi.org/10.1007/s11858-021-01316-4
Marakana, M., Parmar, A. y Shah, P. (2021). A Smart Android Application with Machine Learning Extension to Operate Computer and IoT Devices. En 2021 2nd International Conference for Emerging Technology (INCET) (pp. 1-5). https://doi.org/10.1109/INCET51464.2021.9456382
Marbouti, F. y Strobel, J. (2013). Prototyping an Interactive Application to Support Collaborative Open-Ended Problem Solving for Precollege Students. En 2013 ASEE Annual Conference & Exposition (pp. 23.1005.1-23.1005.8).
Mentzer, N., Huffman, T. y Thayer, H. (2014). High school student modeling in the engineering design process. International Journal of Technology and Design Education, 24, 293-316. https://doi.org/10.1007/s10798-013-9260-x
Niss, M. (2017). Obstacles Related to Structuring for Mathematization Encountered by Students when Solving Physics Problems. International Journal of Science and Mathematics Education, 15, 1441-1462. https://doi.org/10.1007/s10763-016-9754-6
Niss, M. y Blum, W. (2020). The Learning and Teaching of Mathematical Modelling. Routledge. https://doi.org/10.4324/9781315189314
Fonseca, S. (2023). Experiencias Docentes Metodología para la enseñanza de la modelación matemática de problemas de la profesión, vía ecuaciones diferenciales. Pensamiento Matemático, 13(1), 25-37.
Popa, C. R. (2017). High output dynamic range exponential function synthesizer. Microelectronics Journal, 63, 123-130. https://doi.org/10.1016/j.mejo.2017.03.013
Ren, Y., Allenmark, F., Müller, H. J. y Shi, Z. (2021). Variation in the "coefficient of variation": Rethinking the violation of the scalar property in time-duration judgments. Acta Psychologica, 214, art. 103263. https://doi.org/10.1016/j.actpsy.2021.103263
Recio, R. (2018). ¿Cómo cambiar las creencias y el pensamiento utilizando los contenidos de la modelación matemática en la formación de ingenieros? Roca: Revista Científico-Educaciones de la provincia de Granma, 14(5), 106-117. https://dialnet.unirioja.es/servlet/articulo?codigo=6759989
Sánchez, M., Fernández, M. y Díaz, J. (2021). Técnicas e instrumentos de recolección de información: análisis y procesamiento realizado por el investigador cualitativo. Revista Científica UISRAEL, 8(1), 107-121. https://doi.org/10.35290/rcui.v8n1.2021.400
Sansolis, E. B. y Leonoras, C. S. (2021). Viability of a technology-based education afterschool program. Technium. Social Sciences Journal, 19. https://techniumscience.com/index.php/socialsciences/article/view/3170
Stošić, L., Dermendzhieva, S. y Tomczyk, L. (2020). Information and communication technologies as a source of education. World Journal on Educational Technology: Current Issues, 12(2), 128-135. https://doi.org/10.18844/wjet.v12i2.4815
Sudarno y T Widiharih (2021). Determination parameter of exponential function based positive number. Journal of Physics: Conference Series, 1943, art. 012152. https://doi.org/10.1088/1742-6596/1943/1/012152
Sulakono, B., Sarkum, S., Munandar, M., Masrizal, M. e Irmayani, D. (2020). The Diversity of Labuhanbatu Community Culture in Android-Based Applications. International Journal of Advances in Data and Information Systems, 1(2), 60-68. https://doi.org/10.25008/ijadis.v1i2.182
Tolan, S., Pesole, A., Martínez Plumed, F., Fernández Macías, E., Hernández Orallo, J. y Gómez, E. (2021). Measuring The Occupational Impact of AI: Tasks, Cognitive Abilities and AI Benchmarks. Journal of Artificial Intelligence Research, 71, 191-236. https://doi.org/10.1613/jair.1.12647
UNESCO (2022). Educación superior. https://www.unesco.org/es/higher-education
Vesga, G. y De Losada, M. (2018). Creencias epistemológicas de docentes de matemáticas en formación y en ejercicio sobre las matemáticas, su enseñanza y aprendizaje. Revista Colombiana de Educación, (74), 243-267. https://doi.org/10.17227/rce.num74-6909
Xu, Q., Wang, N., Tian, B., Xing, L. y Bai, W. (2020). Challenges and Countermeasures of Education in the Era of Big Data. En PICEIT 2020: Proceedings of the 2020 9th International Conference on Educational and Information Technology (pp. 215-218). https://doi.org/10.1145/3383923.3383964