Implementación de una propuesta didáctica de trigonometría diseñada en GeoGebra

Implementation of a trigonometry didactic proposal designed in GeoGebra

Florencia Díaz Landaverde*

Cecilia Hernández Garciadiego

Universidad Autónoma de Querétaro, Santiago de Querétaro, México

*florencia.diaz@uaq.mx

Licencia Creative Commons Reconocimiento‑NoComercial‑CompartirIgual 4.0
Internacional (CC BY‑NC‑SA 4.0).

Resumen

Se presentan los resultados de la implementación de una propuesta didáctica en el campo de trigonometría diseñada en el software GeoGebra.Se implementó con estudiantes del bachillerato Plantel Concá de la Universidad Autónoma de Querétaro (UAQ), así como alumnos de primer semestre de la Licenciatura en Animación Digital (LAD) perteneciente a la Facultad de Ingeniería. En ambos niveles se integró el uso de las tecnologías de la información y comunicación (TIC) a la enseñanza de la trigonometría. La propuesta constó de dos situaciones, en que se planearon actividades sustentadas en la teoría de situaciones didácticas. El estudio se propone demostrar cómo a partir de la intervención didáctica apoyada en GeoGebra, y de las situaciones planteadas, es posible originar un ambiente de aprendizaje para la construcción y el análisis de las funciones trigonométricas. Según los datos obtenidos, los estudiantes de bachillerato relacionaron conprecisión los conceptos de la trigonometría; asimismo, entendieron el proceso de construcción de las gráficas de las funciones trigonométricas gracias al software GeoGebra; por otra parte, los alumnos de licenciatura reafirmaron sus conocimientos respecto a esta área.

Palabras clave: funciones trigonométricas, GeoGebra, intervención didáctica, teoría de situaciones didácticas, TIC, trigonometría.

Abstract

The results of the implementation of a didactic proposal in the field of trigonometry, designed using GeoGebra software, are presented. It was carried out with high school students from the Conca campus of the Autonomous University of Queretaro (AUQ), and a group of first semester students of the Degree in Digital Animation (DDA) belonging to the Faculty of Engineering of AUQ. At both levels, information and communication technologies (ICT) were incorporated into the teaching of trigonometry. The proposal consisted of two scenarios with activities based on the Theory of Didactical Situations (TDS). This studyaims to demonstrate how, through the didactic intervention supported by GeoGebra and the proposed scenarios, it is possible to establish a learning environment for the construction and analysis of trigonometric functions. According to the data gathered, the high school students accurately related the concepts of trigonometry; similarly, they understood the process of constructing trigonometric function graphs thanks to the GeoGebra software. On the other hand, the undergraduate students reinforced their knowledge in this area.

Keywords: trigonometric functions, GeoGebra, didactic intervention, theory of didactic situations, ICT, trigonometry.

Introducción

La trigonometría es una rama de las matemáticas que a los estudiantes les resulta ardua (De Kee et al., Mura y Dionne, 1996; Maldonado, 2005), quizás debido a su complejidad, suvínculo con numerosos tipos de fenómenos y sus interconexiones con otras disciplinas (Brown, 2005). Dicha dificultad podría perjudicar las diferentes vías del entendimiento y la representación de sus fundamentos (Martín, 2013), tales como los modos de acercamiento y las nociones correspondientes a circunferencia goniométrica (o unitaria), triángulos rectángulos y funciones trigonométricas. Con base en ese impedimento, se percibe un elevado índice de alumnos que carecen de los aprendizajes requeridos (OECD, 2019), lo cual indica que son insuficientes las capacidades de los estudiantes de nivel bachillerato en los ejes matemático y de razonamiento. Ante un problema matemático, tal laguna les impide formular y argumentar la solución utilizando un lenguaje verbal y la terminología correspondiente, menos aún interpretar gráficas. A su vez, cuando avanzan a un nivel educativo superior, la trigonometría les presenta un desafío colosal.

La enseñanza de la trigonometría desempeña un papel decisivo en el currículo escolar en nivel secundaria. Empero, León (2011) refiere que en el ámbito escolar es común encontrar actividades relacionadas con la trigonometría desprovistas de significado para el estudiante. Tal como afirma Maldonado (2005), durante la educación secundaria, la enseñanza de esta materia se limita, en preocupante medida, al cálculo de razones para un ángulo particular. Del mismo modo, los conceptos de ángulo y razón trigonométrica son de significado confuso. De Kee et al (1996) reportan que la comprensión de algunos conceptos como seno y coseno no terminan de asentar en los estudiantes, quienes tienen dificultades para distinguir los triángulos rectángulos de otros tipos. Por otra parte, tampoco diferencian entre una relación trigonométrica y una proporcional: aplican las razones trigonométricas a triángulos no rectángulos, y no se profundiza el concepto de función trigonométrica (Maldonado, 2005).

Resulta propicia la enseñanza en el nivel básico para que los alumnos comprendan los principios de la trigonometría y sean capaces de adentrarse en el estudio de la misma durante el nivel medio superior. Bajo esa premisa, el docente debe emprender la búsqueda de estrategias didácticas que contribuyan a perfeccionar su método (Solanilla, 2015), de modo que su enseñanza sea motivadora y aproveche los recursos tecnológicos a su alcance (Miranda, 2015). En últimas, el objetivo consiste en que los pupilos se apropien de los conocimientos. Por dichos motivos se ha incorporado sistemáticamente en la educación el uso de las TIC (tecnologías de la información y comunicación), las cuales ofrecen experiencias de aprendizaje significativo (Zenginet al, 2012). De la misma manera, como lo señala Donoso (2011), utilizarlas resulta eficaz para la comprensión de ejercicios, la resolución de problemas y el fomento de la creatividad. En consecuencia, se ha considerado implementarlas como método evaluativo de la comprensión trigonométrica en alumnos de niveles superior y medio superior.

En la actualidad, la forma de aprender ha cambiado y resulta necesario modificar en respuesta las técnicas de enseñanza (Marcilla de Frutos, 2013). Este artículo busca introducir una propuesta didáctica de trigonometría basada en actividades y de- sarrollada con el software GeoGebra. Esta plataforma permite al alumno descubrir fenómenos matemáticos, de modo que pueda visualizar la trigonometría de forma didáctica y fortalecer sus destrezas. Al mismo tiempo, al profesor le ofrece una herramienta para crear actividades que incorporan múltiples representaciones de conceptos matemáticos (Rojano, 2003).

La propuesta aborda lo referente a segmentos, líneas y ángulos, para luego formar triángulos rectángulos, analizar sus vértices y formular las razones trigonométricas; luego se abre el camino al círculo unitario y a las funciones trigonométricas.El propósito es presentar los resultados de la implementación didáctica, en aras de evidenciar que el diseño y la aplicación de la propuesta didáctica favorecen la enseñanza-aprendizaje en temas complejos, como es la instancia específica de la trigonometría.

Marco teórico

Este trabajo se basa en la teoría de situaciones didácticas (TSD) de Guy Brousseau, la cual es un modelo constructivista amplio sobre la enseñanza y el aprendizaje de las matemáticas. Conforme a Olguín (2016), es un referente que hace posible el diseño de una secuencia didáctica y su análisis enfocado a la investigación. En la TSD intervienen elementos como el saber-enseñar, y actores como el alumno, quien debe construir su conocimiento, y el profesor, que facilita el medio para ello. La TSD está sustentada en una concepción constructivista en el sentido piagetiano del aprendizaje:

El alumno aprende adaptándose a un medio que es factor de contradicciones, de dificultades, de desequilibrios, un poco como lo hace la sociedad humana. Este saber, fruto de la adaptación del alumno, se manifiesta por respuestas nuevas que son la prueba del aprendizaje. (Brousseau, 1986, como se citó en Olguín, 2016, p. 27)

Por tanto, hay que considerar lo ya descrito por Rotaeche (2008), es decir que que una situación didáctica se considera como la organización del medio efectuada por el profesor. La intención es que el estudiante aprenda un contenido determinado y comprenda las interacciones entre los actores del sistema didáctico, caracterizadas por los contratos didáctico, pedagógico y escolar. En suma, debe existir un compromiso recíproco entre el docente y alumno que establezca los objetivos y contenidos del curso, el método de enseñanza y la forma de evaluación (Brousseau, 1986).

De acuerdo con Chavarría (2006), las situaciones didácticas se refieren al contexto donde el docente presenta el medio para que el alumno construya su conocimiento, donde interactúan los elementos del triángulo didáctico. Están orientadas a desembocar en una situación adidáctica: un proceso donde el estudiante confronta un problema y lo resuelve sin la intervención del docente, construyendo con autonomía su conocimiento. La situación didáctica se desenvuelve en las siguientes fases: la situación-problema (o acción), donde el estudiante interactúa con el medio didáctico para llegar a la resolución de problemas y adquirir conocimientos (Castro et al., 2018); la formulación, que se trata de enfrentar a un grupo de estudiantes con un problema dado y hacerlos partícipes del proceso (Chavarría, 2006); la validación, la cual corresponde al momento donde se evalúa el producto obtenido. Asimismo, la fase final de institucionalización representa la generalización de las actividades y producciones de los estudiantes, donde ellos toman el objeto del conocimiento (Castañeda et al., 2012). Se obtienen conclusiones a partir de las producciones de los alumnos, estableciendo relaciones con el acervo cultural. Es así que, en el diseño de la propuesta didáctica, se adoptó como directriz elpostulado de Brousseau, y se aplicaron los conceptos de razón y función trigonométricas, así como de círculo unitario.

Metodología

La intervención se ejecutó en dos grupos de estudiantes:

• El primero, de 16 a 18 años de edad, perteneciente al cuarto semestre de la Escuela de Bachilleres del Plantel Concá.
• El segundo, de entre 18 y 19 años, perteneciente al primer semestre de la Licenciatura en Animación Digital (LAD).

La muestra total fue de 29 alumnos; ambos programas educativos se desenvuelven en la Universidad Autónoma de Querétaro. Acerca de los tiempos para la implementación de la propuesta didáctica, se realizaron dos fases: la primera de forma presencial con los alumnos de bachillerato y la segunda en modalidad virtual con los de LAD.

Propuesta didáctica

El término intervención didáctica se entiende como la labor del profesor desde una postura de mediador y facilitador del aprendizaje del pupilo (Intervención docente, s. f.). Su finalidad es la transformación de la práctica, la innovación mediante la cual los estudiantes logren el aprendizaje (Pérez, 2014). De esta manera, la importancia de aprender a enseñar se manifiesta en la formación y práctica del docente, en su preparación y compromiso. A través de la reflexión posterior, identificará las áreas de oportunidad de su alumnado, y en consecuencia podrá trabajar para alcanzar niveles satisfactorios de enseñanza y aprendizaje (Rodríguez, 2017). Esas son las directrices que guían el diseño y la implementación de la propuesta didáctica destinada al tema de funciones trigonométricas. Para llevarla a cabo, se plantearon dos situaciones:

1) Calcular las funciones trigonométricas de algunos ángulos a partir de la definición basada en el círculo trigonométrico, con ayuda del software en la computadora.

2) Identificar las gráficas correspondientes a cada función trigonométrica étar por medio del análisis de sus rasgos particulares.

Cada intervención se abordó en un lapso predefinido de 50 minutos. En cada una de las situaciones se instauraron secciones de inicio, desarrollo y cierre. Se abrió con actividades introductorias de los conceptos para inducir al alumno a la comprensión del tema. Posteriormente, en la etapa de desarrollo, se realizaron acciones detonadoras para motivar y captar la atención del participante conforme al objetivo de la situación; para concluir, se llevaron a cabo las tareas de cierre, donde se cotejaron los conocimientos previos con los aprendizajes logrados tras la compleción de las etapas anteriores.

Actividades de introducción

Los estudiantes trabajaron sobre la actividad respondiendo a preguntas introductorias acerca de la definición de ángulo (Figura 1) y las características del círculo unitario a partir de sus conocimientos previos o de la visualización de construcciones preestablecidas. También se les cuestionó respecto a los términos periodo y amplitud de una función trigonométrica (Figura 2). Estas tareas corresponden a la situación-problema o acción de la TSD.

Figura 1. Definición de conceptos como actividad de inicio.

Figura 2. Actividad de inicio.

Actividades de desarrollo

A partir de construcciones hechas en el software, los estudiantes contestaron las preguntas indicadas en cada una de las actividades de la propuesta didáctica (Figura 3). Esta etapa alude a la formulación de la TSD.

Figura 3. Actividades de desarrollo.

Además de realizar las construcciones y dar respuesta a las preguntas, los estudiantes interactuaron en el software, desplazando líneas perpendiculares para observar el ángulo comprendido entre los catetos y la dimensión de cada uno de estos en el triángulo rectángulo (Figura 4). La aplicación hace posible desplazar los vértices A y C para modificar el valor de α (ubicado en la intersección de los segmentos AD y AC) y sus respectivas relaciones trigonométricas, al igual que la longitud de AC y CD.

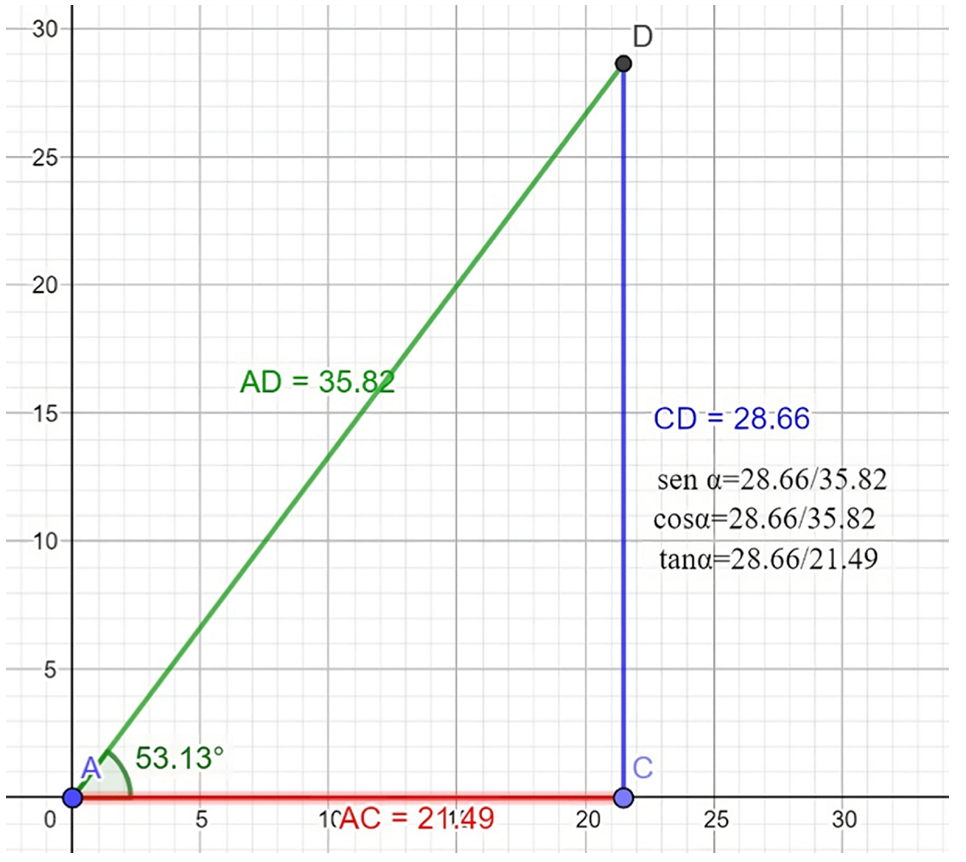
Figura 4. Construcciones hechas de acuerdo con la situación 1.

La Figura 5 corresponde a la realización de construcciones considerando valores de ángulos. Gracias a la animación en el software, fue posible apreciar cómo cam-biaban el signo y valor de las funciones trigonométricas. Se muestran un ángulo de referencia y uno normal. El deslizador verde de α adopta valores de 0 a 90°; el rojo asigna a β valores de 0 a 360°.

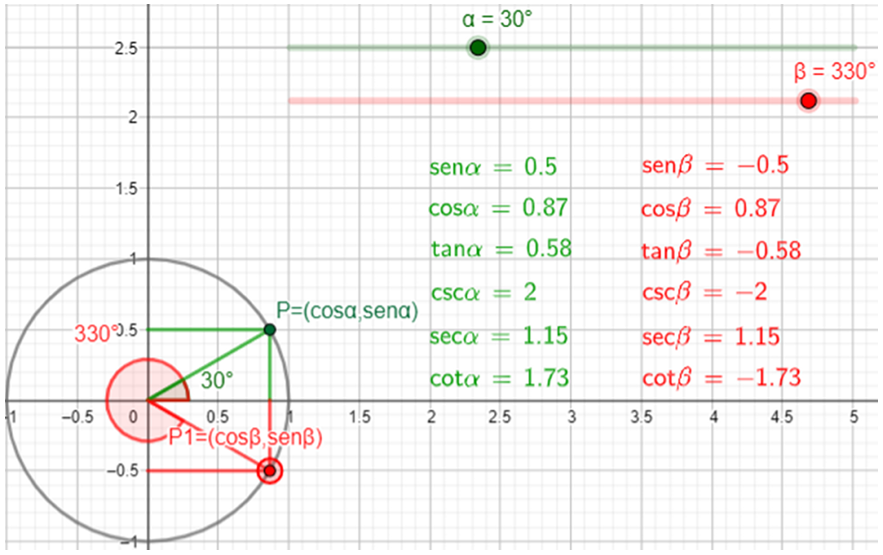
Figura 5. Construcciones hechas de acuerdo con la situación 2

Actividades de cierre.

En última instancia, para evaluar el cumplimiento del objetivo propuesto de cada situación, estas se realizaron mediante la versión en línea de GeoGebra. Para tal fin fueron diseñadas como lecciones con indicaciones precisas, y se proporciona-ron a los estudiantes las ligas correspondientes a las actividades con el código de acceso necesario (Tabla 1).

Tabla 1.

Ligas de acceso para las actividades de cierre.

Resultados y discusión

En adelante se describen las respuestas emitidas por los estudiantes de ambos niveles educativos y se comparan con las esperadas. Se evalúa el desempeño en función de la concordancia entre ambos tipos, y el análisis respeta el orden de las situaciones indicadas en la propuesta didáctica.

En algunos reactivos, respondieron según sus nociones previas adquiridas en el nivel medio superior, como fue el caso de la definición de ángulo (Figura 6). Evo-caron términos como intersección de recta o segmentos, además de la clasificación basada en la medida de los ángulos. Sin embargo, algunos conceptualizaron el ángulo necesariamente como parte de una figura geométrica; otros participantes también requirieron visualizar las construcciones antes de emitir sus definiciones.

En la instancia ilustrada en la Figura 6, además de reconocer que la unidad de medida de los ángulos en el sistema sexagesimal son los grados, el participante afirma correctamente que una revolución corresponde a 360°.

Figura 6. Definición de ángulo según un participante.

En las construcciones presentadas, la mayoría identificó que correspondían a la clasificación de triángulo rectángulo; no obstante, algunos expresaron otras categorizaciones que, aunque correctas, no conservaban relevancia en la tarea actual (Figura 7). Un alto porcentaje de estudiantes no avistó que en un triángulo rectángulo hay dos ángulos agudos y uno recto, en cambio aludieron a un solo tipo, tal como se observa en la Figura 8.

Figura 7. Identificación del tipo de ángulo.

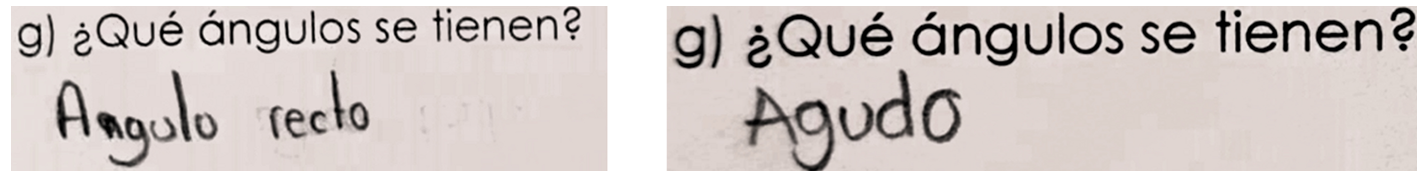Figura 8. Identificación de un solo ángulo en un triángulo rectángulo.

La actividad 3 de la situación 2 requería visualizar el círculo unitario y evaluar las coordenadas de un punto P. Y pese a que algunos estudiantes estaban en nivel superior, tuvieron dificultad para percatarse de que las coordenadas del punto P eran (cos α, sen α) (Figura 9); es decir, no advirtieron que las longitudes de los catetos del triángulo rectángulo en el círculo unitario equivalen a las funciones seno y coseno del ángulo α.

Figura 9. Valor numérico de la abscisa del punto P.

De forma paralela, en la actividad referente a evaluar el valor natural y los signos de las funciones trigonométricas de la situación 2, mostraron dificultad para discernir entre el ángulo normal y el de referencia (Figuras 10 y 11). La omisión resulta comprensible, al menos para los alumnos de bachillerato, ya que aborda-ron el curso de trigonometría superficialmente, dada la modalidad de las clases durante la pandemia de covid-19.

Figura 10. Definición incompleta del ángulo normal.

Figura 11. Definición de ángulo de referencia.

Una vez que construyeron las gráficas de las funciones trigonométricas, fueron capaces de identificar y comprender las características de las funciones mediante la animación, así como observar el correlato gráfico en el software (Figura 12).

No obstante, es claro que algunos estudiantes no dilucidaron por completo cómo indicar las características de la gráfica, por ejemplo, señalar si existen asíntotas o definir el dominio, los intervalos de incremento o disminución, y la amplitud de cada onda (Figura 13).

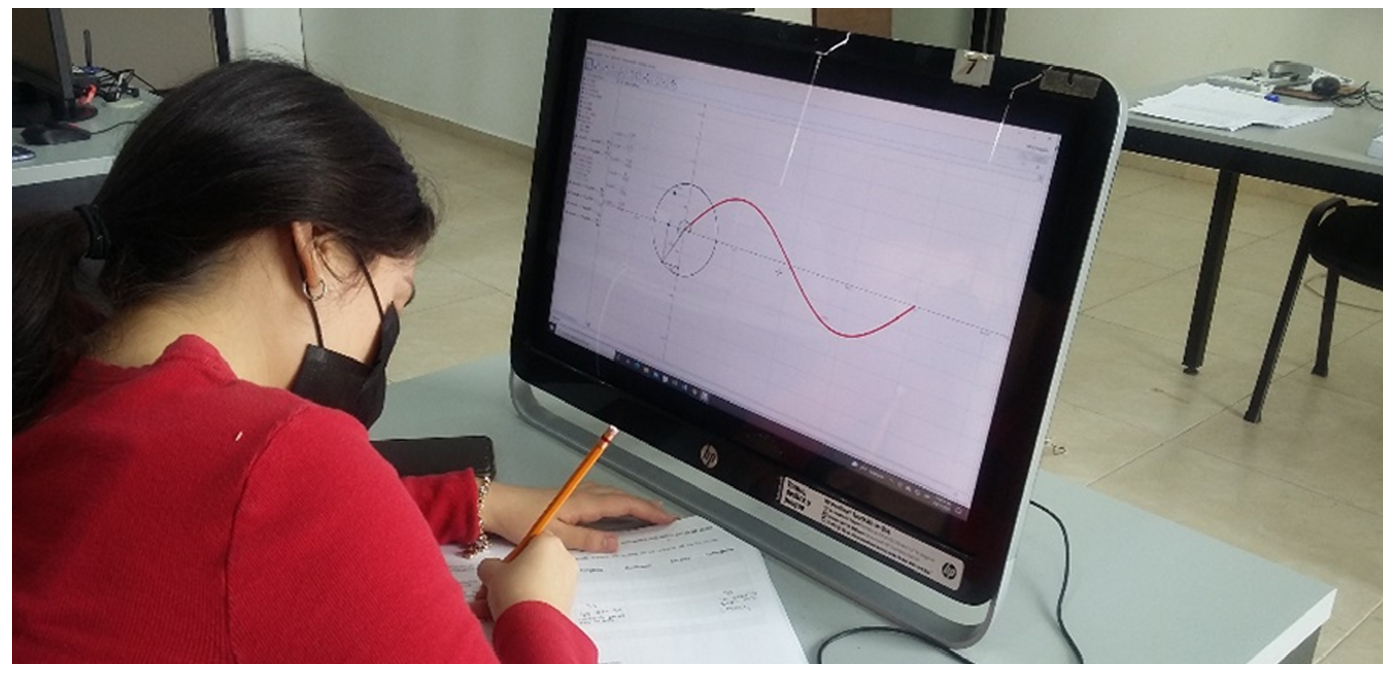Figura 12. Animación de la función seno.

Figura 13. Características de las funciones trigonométricas.

Cabe destacar que los participantes de LAD ostentan una noción más acertada de lo que es periodo. Por su parte, los alumnos de bachillerato describieron con mayor precisión las características de las gráficas; la mayoría de los estudiantes definieron la amplitud como un concepto que refiere a la distancia entre el eje de las abscisas y el punto más alto de la onda. Por otro lado, un grupo reducido refirió a la cresta de una onda (“el punto máximo”) y su valle (“el punto mínimo). En este sentido, la primera descripción fue la más satisfactoria.

Figura 14. Definición de amplitud en una función trigonométrica.

Por último, se presentan los resultados de cierre de cada actividad (Figura 8) correspondiente a las situaciones. Se observa que la participación de ambos grupos en las actividades fue menguante, en especial la de los estudiantes de LAD, debido a la modalidad en que se llevó a cabo la propuesta didáctica, como se mencionó anteriormente.

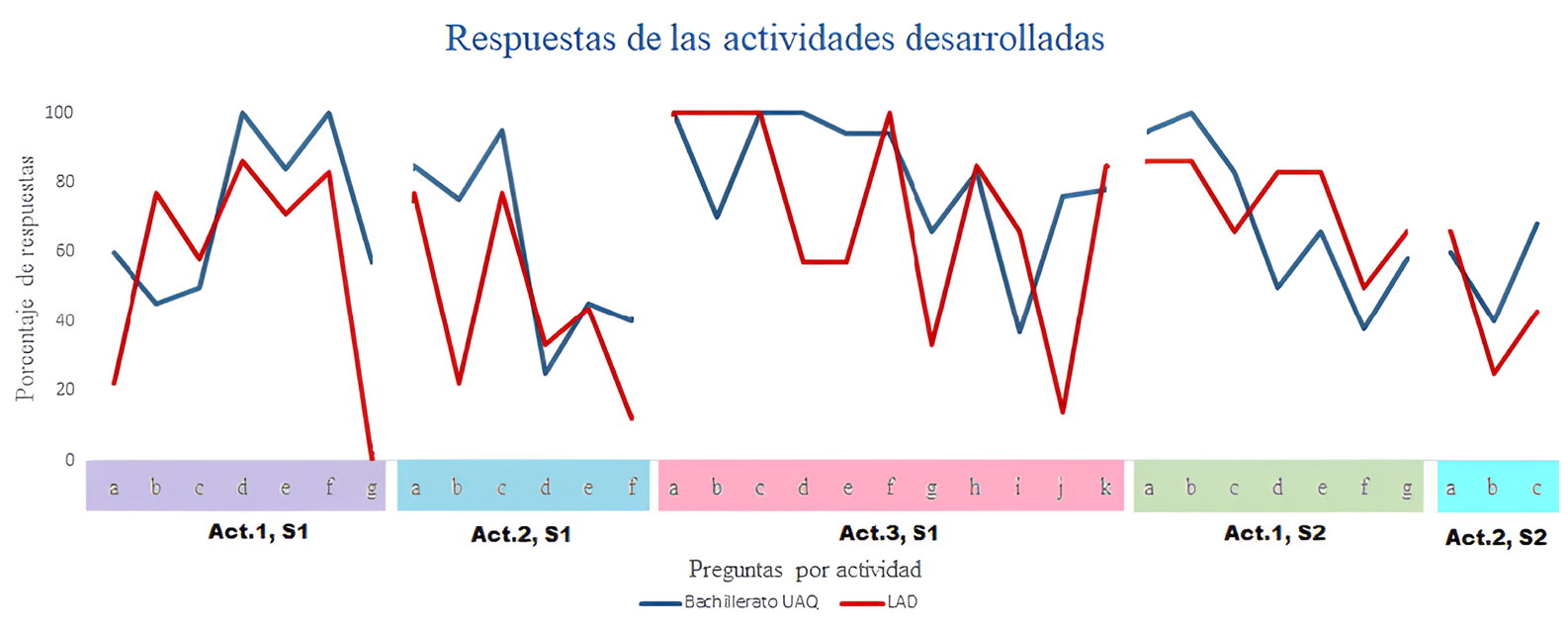Figura 15. Resultados de las actividades de cierre.

En el caso de los alumnos de bachillerato, la interacción con las construcciones fue clave, pues les permitió visualizar la relación de los segmentos del triángulo rectángulo y los ángulos que lo conforman. De la misma manera, pudieron comprobar cómo a medida que se abren o cierran los ángulos se alteran las coordenadas del punto P, y corroborar los signos en los diferentes cuadrantes para cada de una de las funciones. Desde esta perspectiva, la interacción logró su cometido: permitir a los estudiantes complementar su conocimiento en trigonometría.

Conclusiones

Los resultados permiten concluir que el grupo de bachillerato fue más acertado al contestar las preguntas indicadas en el desarrollo de actividades por cada situación. Es destacable que la interacción con el software les permitió asimilar con mayor claridad cómo se construyen las gráficas de las funciones trigonométricas mediante rectas, segmentos, puntos, ángulos y círculos unitarios. Conviene resaltar que la participación del grupo en modalidad presencial fue fructífera, en virtud de que siguieron las indicaciones de la propuesta, realizaron por sí mismos las construcciones en GeoGebra y participaron activamente, pese a que desconocían el uso de la plataforma. El empleo de la tecnología permeó de manera positiva el proceso de enseñanza-aprendizaje de los pupilos. Si bien la actividad goza de instrucciones específicas, fue preciso cuestionar a los participantes para fomentar su exploración e interacción con la plataforma. De esa manera, lograron discernir consideraciones particulares en trigonometría, por ejemplo, la correspondencia de valores naturales de los ángulos notables o los signos de las funciones trigonométricas en cada uno de los cuadrantes.

En términos del nivel educativo de los participantes, se percibió una diferencia actitudinal importante entre los dos grupos. Por un lado, los bachilleres mostraron un involucramiento proactivo en las tareas; por el contrario, los alumnos de LAD manifestaron un escaso compromiso, y renuencia a desarrollar las actividades. En otro sentido, las modalidades empleadas fueron un factor prominente en los resultados. Con respecto al grupo de estudiantes de bachillerato, las actividades presenciales ayudaron a mantener orden en el aula, agilizaron los cuestionamientos y permitieron orquestar respuestas concretas, e incluso respetar los tiempos designados para cada sesión. En el caso del grupo de LAD, que se desenvolvió en modalidad virtual, se detectó poca disposición en los tiempos de entrega y en la seriedad al responder los reactivos; aunado a esto, no se realizaron las actividades de cierre por completo.

La implementación de esta propuesta didáctica ha develado áreas de oportunidad para la práctica docente; integrarla como parte del desarrollo de las clases podría facilitar el abordaje de la trigonometría, de forma específica el paso de las razones trigonométricas a las funciones trigonométricas. La meta es que exista una comprensión profunda del tema desde el nivel medio superior, ya que fue evidente que los alumnos de licenciatura aún atraviesan atolladeros en esta materia. Para continuar y expandir el estudio de este tema, se sugiere enriquecer el acervo de actividades realizables en GeoGebra a fin de asociar las características de las funciones trigonométricas con temas pertenecientes a otras disciplinas. De tal manera, sería posible dotar de sentido las matemáticas en el contexto cotidiano. Como planteamiento final, quizás pueda establecerse una comunidad de docentes que compartan dicho material de forma libre, siempre que se atribuyan los créditos pertinentes a los autores y se realice sin fines de lucro.

Referencias

Brousseau, G. (1986). Fondements et méthodes de la didactique des mathématiques. Recherches en Didactique des Mathématiques, 7(2), 33-115.

Brown, S. A. (2005). The trigonometric connection: Students’ understanding of sine and cosine [Tesis de doctorado, Illinois State University]. https://www.proquest.com/openview/2f8f9e2a6508f98b8e8b382a0109daca/1?cbl=18750&diss=y&pq-origsite=gscholar&cbl=18750&diss=y

Castañeda Alonso, A., Rosas Mendoza, A. y Molina Zavaleta, J. G. (2012). La institucionalización del conocimiento en la clase de matemáticas. Un estudio sobre el discurso del aula. Perfiles Educativos, 34(135). https://doi.org/10.22201/iisue.24486167e.2012.135.29169

Castro López, C. E., Arteaga Moreno, J. A. y Ricaurte Urbano, L. A. (2018). Situaciones didácticas en la enseñanza de las razones trigonométricas en estudiantes de grado décimo [Tesis de maestría, Universidad del Cauca]. http://repositorio.unicauca.edu.co:8080/xmlui/handle/123456789/395

Chavarria, J. (2006). Teoría de las situaciones didácticas. Cuadernos de Investigación y Formación en Educación Matemática, 1(2).

De Kee, S., Mura, R. y Dionne J. (1996). La compréhension des notions de sinus et de cosinus chez des élèves du secondaire. For the Learning of Mathematics, 16(2), 19-27.

Díaz Fernández, M. T. (2014). Enseñanza de trigonometría en 4^o de la ESO con GeoGebra [Tesis de maestría, Universidad Internacional de la Rioja]. https://reunir.unir.net/handle/123456789/2426

Donoso, C. (2011). Introducción al Nuevo Bachillerato Ecuatoriano. https://educacion.gob.ec/wp-content/uploads/downloads/2013/03/SiProfe-BGU-Introduccion.pdf

Herrera, H. (2013). Enseñanza de los conceptos básicos de la trigonometría mediante el uso de la tecnología informática [Tesis de maestría, Universidad Nacional de Colombia]. https://repositorio.unal.edu.co/handle/unal/21149

León, C. E. (2011). El paso de la razón a la función trigonométrica: revisión de algunos elementos históricos en la construcción de la función trigonométrica. En P. Perry (Ed.), Memorias del 20º Encuentro de Geometría y sus Aplicaciones (pp. 371-378). Universidad Pedagógica Nacional.

Maldonado, E. (2005). Un análisis didáctico de la función trigonométrica[Tesis de maestría]. Cinvestav-IPN.

Marcilla de Frutos, C. (2013). Las TIC en la didáctica de las matemáticas [Tesis de maestría, Universidad de Burgos]. https://riubu.ubu.es/bitstream/handle/10259.1/182/Marcilla_de_Frutos.pdf;jsessionid=B4CDC475A0AF18F67F11917D28C36EDB?sequence=1

Martín, E. (2013). Significados puestos de manifiesto por estudiantes de Bachillerato respecto al concepto de razón trigonométrica [Tesis de maestría]. Universidad de Granada.

Martínez, J. y Martínez, G. (2007). La didáctica y la cognición de los ángulos negativos y mayores a 360º y sus funciones trigonométricas: un estudio en el nivel medio superior. Acta Latinoamericana de Matemática Educativa, 20. https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1214333/Mart25C325ADnezLadid25C325A1cticaALME2007.pdf

Miranda, L. I. (2015). Uso de Recursos Educativos Abiertos en el aprendizaje de las funciones trigonométricas [Tesis de maestría, Instituto Tecnológico de Monterrey y Universidad Autónoma de Bucaramanga]. https://repository.unab.edu.co/bitstream/handle/20.500.12749/3136/2015_Tesis_Miranda_Huertas_Liliana_Isabel.pdf?sequence=1&isAllowed=y

OECD (2019). Resultados PISA2018 [Archivo PDF]. https://www.oecd.org/content/dam/oecd/en/about/programmes/edu/pisa/publications/national-reports/pisa-2018/featured-country-specific-overviews/PISA2018_CN_MEX.pdf

Olguín, G. (2016). Una propuesta didáctica para la construcción de las funciones trigonométricas seno y coseno [Tesis de maestría, Universidad de Los Lagos]. https://edumat.ulagos.cl/wp-content/uploads/2019/02/Gonzalo-Olgu%C3%ADn.pdf

Pérez, M. Á. (1997). La intervención didáctica como alternativa para transformar la práctica. Educar. Revista de Educación/Nueva Época, (1).

Rodríguez, H. (2017). Importancia de la formación de los docentes en las instituciones educativas. Ciencia Huasteca Boletín Científico de la Escuela Superior de Huejutla, 5(9). DOI: 10.29057/esh.v5i9.2219

Rojano, T. (2003). Incorporación de entornos tecnológicos de aprendizaje a la cultura escolar: proyecto de innovación educativa en matemáticas y ciencias en escuelas secundarias públicas de México. Revista Iberoamericana de Educación, 33, 135-165. DOI: 10.35362/rie330914

Rotaeche, R. (2008). La construcción del concepto de ángulo en estudiantes de secundaria. Aportaciones para un diseño escolar. [Tesis de maestría no publicada]. Instituto Politécnico Nacional.

Solanilla, O. (2015). Implementación de herramientas didácticas y tecnológicas para mejorar el nivel de aprendizaje de la trigonometría [Tesis de maestría, Universidad del Tolima]. https://repository.ut.edu.co/entities/publication/138bc0eb-1452-48dd-a1c1-62ca9e6a2078

Torres, D. y Montiel, G. (2021). Resignificación de la razón trigonométrica en estudiantes de primer año de Ingeniería. Educación Matemática, 33(3), 202-232. DOI: 10.24844/em3303.08

Universidad de Granada (s. f.). Intervención didáctica.PID-Prácticum E.F.https://www.ugr.es/~rescate/practicum/intervencion_didactica.htm

Zengin, Y., Furkan, H. y Kutluca, T. (2012). The effect of dynamic mathematics software geogebra on student achievement in teaching of trigonometry. Procedia - Social and Behavioral Sciences, 31, 183-187 DOI: 10.1016/j.sbspro.2011.12.038